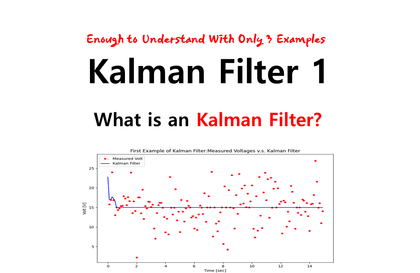
Im Jang-hwan's Kalman Filter 1
jhim21
You can understand the theoretical operation principle of the Kalman Filter through easy examples.
Basic
kalman-filter, Probability and Statistics, Linear Algebra
This is the optimization theory required for AI/deep learning, computer vision, computer graphics, etc. Optimization Theory 1 mainly deals with the definition of multivariable functions and differentiation of multivariable functions. Why is that? Because all optimization problems are expressed in the form of multivariable functions. If you acquire the exact definition of multivariable functions and the concept of differentiation, the theoretical approach in the above fields will become considerably easier.
75 learners
Level Basic
Course period Unlimited

Study the definition of multivariable functions required for optimization theory.
Studying differentiation of multivariable functions
Taylor expansion of multivariable functions
Book: Lecture based on Optimization Theory (written by Im Jang-hwan)
Who is this course right for?
Machine learning, deep learning, computer vision, computer graphics, and engineering people
I recommend this to those who want to properly understand the differentiation of multivariable functions.
I recommend this to those who want to study their major more deeply in graduate school.
Need to know before starting?
Linear algebra, calculus
The will to do it is essential
Those who will invest consistently for one month
212
Learners
9
Reviews
7
Answers
4.7
Rating
4
Courses
박사 졸업 후 5년 정도 Computer vision를 공부하고 가르치는 계기가 돼서
지금까지 수학전공과 공학이론을 연결한 공부들을 하고 있습니다.
전문분야(공부 분야)
전공: 수학(Topological Geometry), 부전공(컴퓨터 공학)
현) 3D Computer Vision(3D Reconstruction) , Kalman Filter, Lie-group(SO(3)),
Stochastic Differential Equation 연구자
현) 유튜브 채널 운영: 임장환: 3D Computer Vision
현) facebook Spatial AI KR 그룹 (수학전문위원)
출신학교
독일 Kile 대학 이학박사 (Topological Geometry & Lie-group 전공, 컴퓨터 공학 부전공)
중앙대 수학과 학사, 석사(Topology 전공)
경력
전) 대성그룹 자회사 두비비젼 CTO
전) 중앙대학교 첨단영상 대학원 연구교수(3D Computer Vsion연구)
저서:
최적화이론: https://product.kyobobook.co.kr/detail/S000200518524
링크
유튜브: https://www.youtube.com/@3dcomputervision
블로그: https://blog.naver.com/jang_hwan_im
All
17 lectures ∙ (3hr 16min)
Course Materials:
All
1 reviews
5.0
1 reviews
Reviews 2
∙
Average Rating 5.0
5
I'm majoring in Artificial Intelligence, and I'm starting to wonder what kind of AI I was actually learning before. After learning the foundational mathematics, the theory became the basis, and I definitely understand the AI I learned much better and gained a deeper understanding. The content isn't too long either, so it's not boring, and it's a great help to go through it once.
Limited time deal ends in 4 days
$38,500.00
30%
$42.90
Check out other courses by the instructor!
Explore other courses in the same field!