2-8 fully connected NN answer 코드 중 torch.nn.Linear 질문드립니다!

Question

안녕하세요. 강의 잘 듣고있습니다 :D 아래 코드에서 torch.nn.Linear에 해당하는 부분이 강의서 말씀해주신 aggregation에 해당되는 부분일까요? 편의상 bias 벡터는 생략된걸까요..? 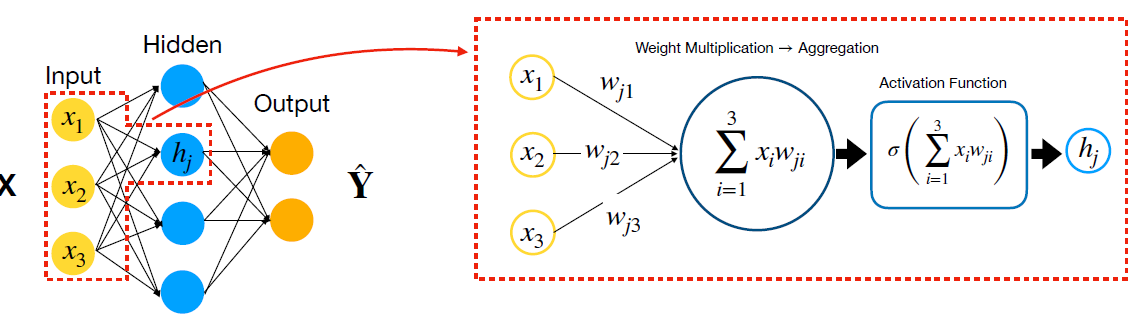class Model(torch.nn.Module) : def __init__(self) : super(Model, self).__init__() self.layers = torch.nn.Sequential( # 첫번째 레이어 torch.nn.Linear(in_features = 128, out_features = 64, bias = True), # 첫번째 레이어의 activation 함수 torch.nn.Tanh(), # 두번째 레이어 torch.nn.Linear(in_features = 64, out_features = 16, bias = True), # 두번째 레이어의 activation 함수 torch.nn.Tanh(), # 세번째 레이어 torch.nn.Linear(in_features = 16, out_features = 1, bias = True), # 세번째 레이어의 activation 함수 torch.nn.Sigmoid() ) def forward (self, x) : return self.layers(x)

변정현 · Answer

안녕하세요, 변정현입니다. 강의를 잘 수강하고 계시다니 저도 뿌듯하네요. 감사합니다. 좋은 질문들 주셔서 감사합니다. 아래 코드에서 torch.nn.Linear에 해당하는 부분이 강의서 말씀해주신 aggregation에 해당되는 부분일까요? torch.nn.Linear은 Weight Multiplication과 Aggregation 둘 다 포함합니다. 섹션 6의 첫번째 Ppt의 22번째 슬라이드 "Forward Pass as Matrix Multiplication"을 보시면 Weight Multiplication 및 Aggregation이 Matrix Multiplication으로 표현된다는 것을 확인할 수 있습니다. 그리고 섹션 2-8 실습편을 보시면 torch.nn.Linear은 사실상 Weight Matrix 곱하기 Input 더하기 Bias로 구성되는 것을 확인할 수 있습니다. 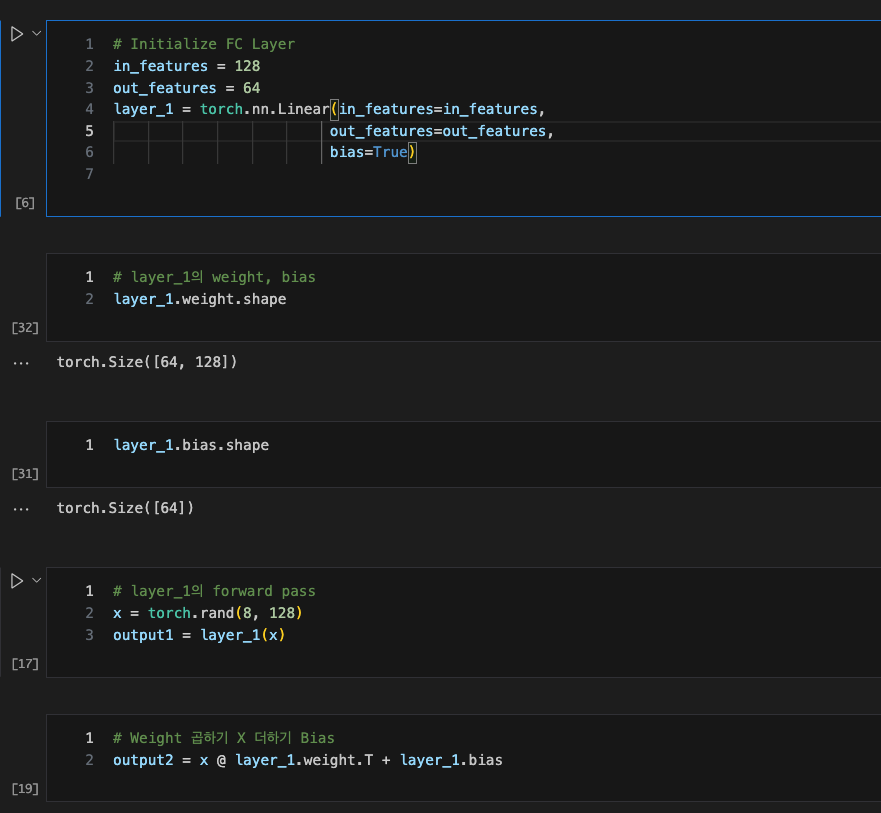편의상 bias 벡터는 생략된걸까요..? 네 편의상 Bias을 생략한 것은 맞습니다. 하지만 한가지 참고사항으로 말씀드리자면, Input X에 차원수를 하나 추가해서 새로운 차원은 1의 값을 가진다고 가정해보겠습니다. 즉, X' = concat( [ X, 1 ] ) 이 되는 셈입니다. 그러면 W X + b 은 사실상 W' X'으로 표현할 수 있습니다. 여기서 W'은 W 행렬에 bias b을 마지막 row로 가지는 행렬입니다. 부연 설명드리자면 W이 M by N 행렬이면 W'은 (M+1) by N 행렬입니다. 1~M번째 row은 W 행렬과 동일하고 마지막 M+1번째 row은 bias vector B 값인 셈이죠. 즉, W' = concat( [ W, b ] ) 입니다. 이렇게 W'과 X'을 정의해서 W' X' 을 곱해보시면 WX + b의 결과와 동일하다는 것을 확인하실 수 있습니다. 따라서 편의상 bias b을 생략한 것은 맞지만 WX + b도 결국에는 WX 와 같은 꼴로 표현될 수 있다는 의미입니다 ㅎㅎ 그래서 딥러닝 논문들이나 교과서들을 보시면 Bias B 를 따로 구분하지 않는 경우가 많습니다.   감사합니다.