인프런 커뮤니티 질문&답변
작성한 질문수
13 표준화에 관한 질문
해결된 질문
작성
·
247
1
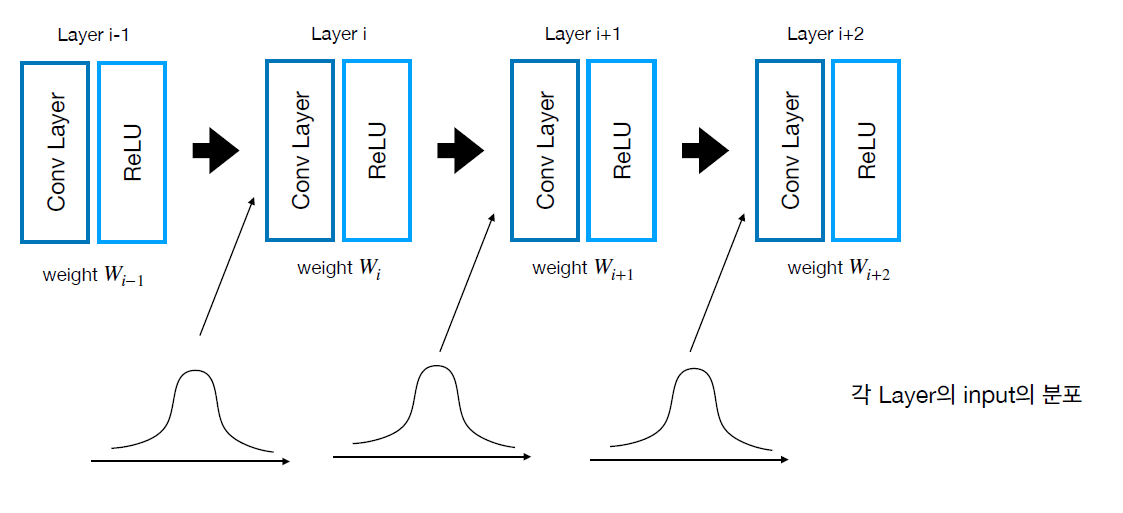1.위의 그림에서 weight가 정규분포(Gaussian distribution)를 따르기 때문에 각 layer의 input의 분포도 정규분포를 따른다고 말씀해주셨는데 그 이유가 궁금합니다..
2.표준화(Z~N(0,1))를 위해서는 확률분포가 정규분포여야 한다고 알고 있습니다..
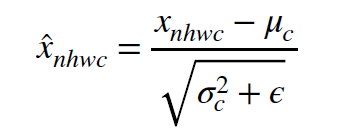
그래서 batch normalization의 위의 식에서 x가 정규분포를 가져야 한다고 생각했는데 학습 데이터셋은 직접 정규분포를 가지게 넣는다고 가정하더라도 그 다음에 있는 convolutional layer의 weight가 gradient descent에 의해 업데이트 되어 더이상 정규분포를 따르지 않으면 출력값이 정규분포를 따르지 않을수도 있지 않을까요...?
답변 1
2
안녕하세요!
좋은 질문들을 주셔서 감사합니다~
첫번째 질문의 경우, 제가 Weight이 He initialize로 초기화되었다는 설명을 드리면서 혼선을 드린 것 같네요.
부연설명드리자면, Weight은 처음에 초기화될때 Normal Distribution으로부터 샘플링된 것으로, 샘플링 된 후에 (즉, 이후 학습의 과정)에서는 특정 값을 가지는 parameter입니다. 반면에 입력값은 학습 과정에서 계속 랜덤하게 샘플링되는 Random Variable이라고 볼 수 있습니다.
그리고 Gaussian 분포를 따르는 Random Variable에 사칙연산들을 적용했을때 Gaussian 분포가 출력되므로 WX+b의 분포도 Gaussian 분포를 따르게 됩니다.
Non-linear한 transformation이 적용된 경우, 변환된 Gaussian 분포는 Gaussian이 아닐 수 있지만 변환이 충분히 smooth하고 입력 분포의 Variance가 작다면 변환된 분포는 대략적으로 Gaussian 분포를 따른다고 볼 수 있습니다.
따라서 각 Layer의 출력값 (즉, 다음 Layer의 입력값) 들은 대략적으로 Gaussian 분포라고 볼 수 있습니다.
두번째 질문의 경우도 마찬가지로, Gradient Descent을 수행한 후에는 Weight parameter 값은 변하고 이에 따라 WX + b 의 평균과 분산은 바뀌지만 출력되는 분포는 여전히 Gaussian입니다.
답변이 도움이 되었으면 좋겠네요 ㅎㅎ
감사합니다!
제가 W를 값으로 보지 않고 하나의 Random Variable로 착각해서 보았군요! 답변 감사합니다!