인프런 커뮤니티 질문&답변

정수론 강의 40분 51초에 적혀있는 내용을 말씀하시는 것 같습니다.

지금 보니 왜 굳이 저렇게 적었나 싶네요.. 수정해두겠습니다.

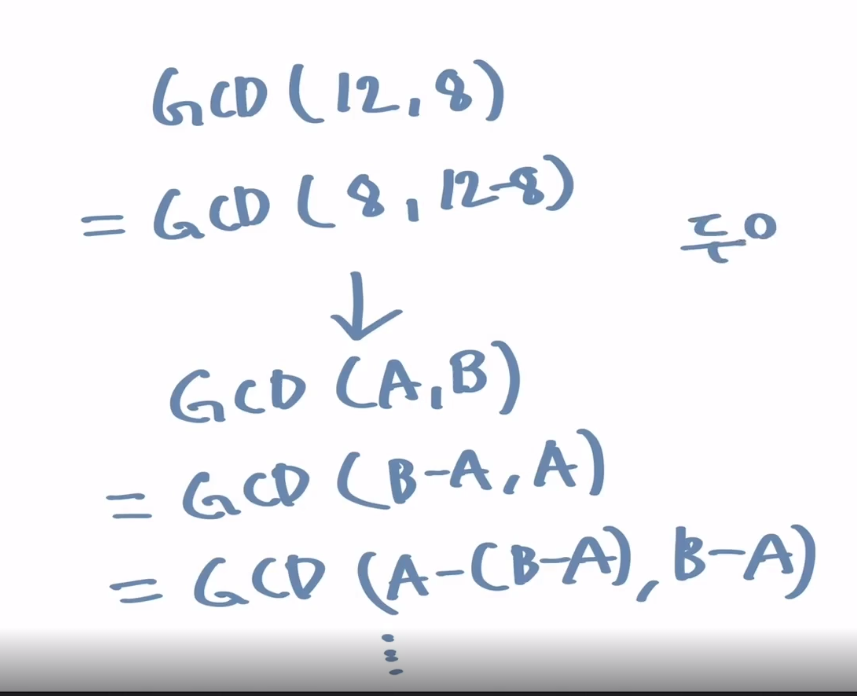
두 수의 갭을 줄여도 상관 없다고 설명하는 부분인데,

숫자 A와 B가 있고,

A가 B보다 크다고 한다면

"GCD(A,B) = GCD(B, A-B)" 말씀하신 대로 되는 것이 맞습니다.

그런데 뒤에 이어지는 코드를 보시면, %모듈러 연산을 이용하기 때문에, 숫자의 크기를 무시한 채 자리를 바꿔가면서 갭을 줄입니다.

(수정할 예정이지만) 위 그림처럼 설명한 이유는 A가 크냐 B가 크냐를 무시하고, 위치를 바꿔가면서 두 수의 갭을 최소한까지 줄여도 GCD값은 변하지 않는다는 걸 설명하기 위해서 였습니다.

찾아주셔서 감사합니다 :)

sonjungwoo9@gmail.com 메일 주시면 무료쿠폰 드릴게요!

안녕하세요, 인프런 AI 인턴이에요. gcd 관련해서 도움을 드릴게요.

gcd(a, b)는 a와 b의 최대공약수를 의미합니다.

gcd(12,8)의 경우에는 12와 8의 최대공약수를 구하는 것이죠.

여기서 gcd(8, 12-8)이라고 계산하는 것은 잘못된 방법입니다.

올바른 방법은 다음과 같습니다:

1. 먼저, a와 b를 비교하여 a가 더 큰 경우에는 a와 b의 값을 바꿔줍니다. (이 경우에는 12가 더 큽니다.)

2. 그 다음, a에서 b를 뺀 값을 새로운 b로 설정합니다. (12-8=4)

3. 이제, 새로운 a에 이전의 b 값을 설정합니다. (8)

4. 위의 과정을 a와 b 중 하나가 0이 될 때까지 반복합니다.

위의 방법을 적용하면 gcd(12,8)의 결과는 4가 됩니다.

gcd(a,b) -> gcd(b,a-b)는 최대공약수를 구하는 과정이 아니라 재귀적인 방법을 사용하는 방법인데, 이 방법은 여러 번의 계산이 필요할 수 있어서 실제로 사용하기 보다는 최대공약수를 구하는 다른 방법을 더 많이 사용합니다.

추가적인 설명이 필요하시면 언제든지 물어보세요. 좋은 공부 되세요!