인프런 커뮤니티 질문&답변

안녕하세요 :)

 

10진수부가 1이 아닌 경우에도 1.ㅁㅁㅁㅁ x 2^△ 꼴의 수로 변환될 수 있습니다.

 

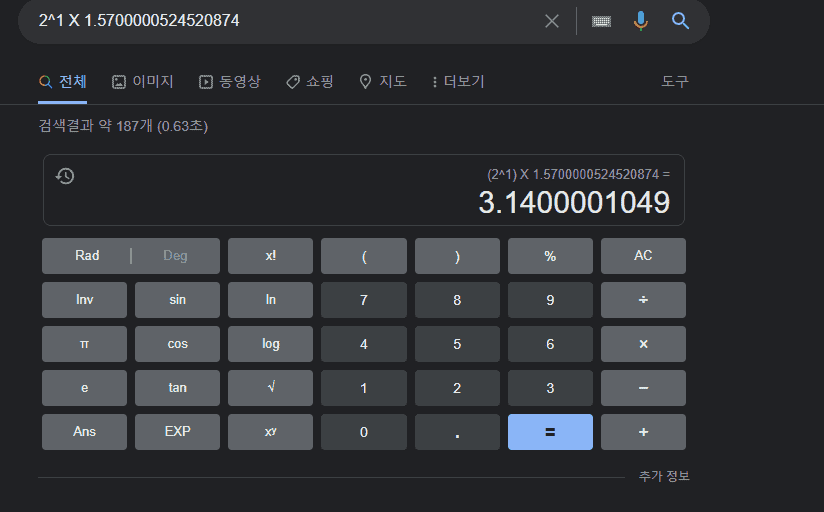
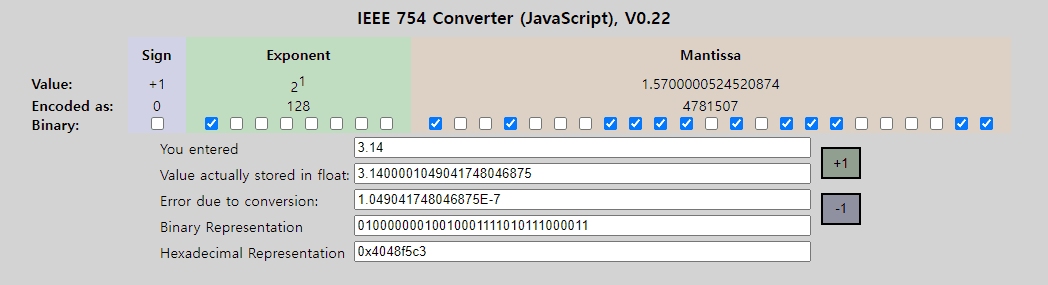
질문 주신 3.14의 경우에도 2^1 X 1.5700000524520874 로 변환될 수 있습니다.

 

 

아래 링크에서 다양한 숫자들을 변환해보시며 확인해보세요 :)

https://www.h-schmidt.net/FloatConverter/IEEE754.html

 

그리고, 한 가지 오개념을 방지해드리고자 첨언 드리자면,

 

3.ㅁㅁㅁㅁx 2^△  형태로는 변환되지 않습니다. 

만일 질문하신 대로 3.ㅁㅁㅁㅁx 2^△ 형태로 변환된다면,

3.ㅁㅁㅁㅁ 부분이 이미 2를 넘었으니,

ㅁ의 숫자가 줄고, 2^△의 △의 수가 올라가겠죠? 

 

사실 이는 질문자님께서 아직 교과과정 수학(지수법칙, 로그)을 공부하지 않으신 학생이시라면 

조금 이해가 어려울 수는 있습니다.

 

컨셉이 난해하다면, 아래 위키피디아 내용처럼 이해하셔도 무방합니다. 

 

https://en.wikipedia.org/wiki/Normalized_number

 

In base b a normalized number will have the form

{\displaystyle \pm d_{0}.d_{1}d_{2}d_{3}\dots \times b^{n},}

where again {\textstyle d_{0}\neq 0,} and the digits, {\textstyle d_{0},d_{1},d_{2},d_{3},\ldots ,} are integers between {\displaystyle 0} and {\displaystyle b-1}.

 

 

즉, 지수가 b인 경우, d들은 (d0을 제외하고) 0부터 b-1까지의 수를 가지는 것이지요. 

 

감사합니다 :)