인프런 커뮤니티 질문&답변
그래프 관련 헷깔리는 부분 질문
작성
·
338
0
https://blog.naver.com/jhc9639/222289089015
강의 블로그글에는 아래와 같은 설명이 있습니다.
정점 Vertex : V
간선 Edge : E
E = V - 1
질문1. 인접행렬(정사각행렬)의 한변의 길이
인접행령의 한 변의 길이를 v라고 하면 인접행렬의 모든 원소 (i, j) 를 탐색하는데 시간적으로 V길이의 제곱에 비례한다는 사실을 이해할 수 있습니다.O(V^2), 공간적으로도 V^2에 비례하여 메모리를 차지할 것입니다.
블로그글 설명 그래프표현방법 에서는 한변의 길이를 v로 놓아 해당 챕터전반에서 다루는 그래프이론에서 쓰이는 정점 V와 혼동을 주는것 같습니다.
질문2. 인접리스트
vector<int> adj[1004];
adj[1].push_back(2); 정점1과 정점2가 연결관계라면 위 코드는 정점1의 연결정보를 담는 vector에 2를 추가한 것이라 보여집니다.
같은 상황으로 정점2입장에서도 정점1이 연결된것으로 해석해 아래와 같은 코드가 항상 같이 작성되야하지 않을까 의문이 듭니다.
vector<int> adj[1004];
adj[1].push_back(2);
adj[2].push_back(1);
질문3. 시간복잡도
인접리스트는 시간복잡도는 O(V + E), 공간복잡도 또한 O(V + E)입니다.
DFS의 경우) 인접리스트로 이루어진 맵이면 O(V + E)이고 인접행렬의 경우 O(V^2)가 됩니다.
BFS의 경우) 인접리스트로 이루어진 맵이면 O(V + E)이고 인접행렬의 경우 O(V^2)가 됩니다.
위 세 문장에 대해 아래와 같은 정리를 해봤습니다.
인접리스트는 인접행렬에 반해 자유분방한 그래프를 표현하기에 최적의 수단이고
vector<NODE> myGraph[10]; 에서 한 노드가 여러 다른 노드와의 연결이 가능하므로
myGraph[0], myGraph[1], myGraph[2] ,,, myGraph[9] 마다 크기가 제각각이다.
따라서 정점 V갯수가 많을 수록, 노드연결 갯수 E가 많을 수록 전체노드를 탐색하는 시간이 늘어난다고 이해했습니다.
따라서, 이때도 V 와 E 의 의미를 정점과 간선으로 잘 이해할 수 있었습니다.
하지만, 인접행렬 O(V^2)은 정사각형 맵이 주어졌을 때 한 변의 길이로 봐야할 것 같습니다. 따라서 표기를 V가 아닌 다른것으로 하는게 맞지 않을까 생각듭니다.
답변 1
0
안녕하세요. ddo님 ㅎㅎ
세심한 부분을 신경써주셔서 감사합니다. ddo님의 의견을 반영해서 헷갈릴만한 부분은 반영해서 수정했습니다. (블로그)
답변은 다음과 같아요.
질문1. 인접행렬(정사각행렬)의 한변의 길이
A1.
음 V는 정점이 맞아요. 한변을 나타내는 것은 아니나 해당 부분 설명 수정했습니다.
위 코드는 a[i][j], 즉 i로부터 j까지 경로가 있다면 "i부터 j까지 경로가 있습니다."를 출력하는 코드입니다. 이렇게 2중 반복문을 통해 쓰입니다.
참고로 해당 코드의 시간복잡도는 O(V^2), 공간복잡도 또한 O(V^2)입니다.
앞의 코드는 보통 이런식으로 쓰입니다. i라는 정점에서 j까지의 정점이 있다면 해당 정점으로 부터 시작되는 "탐색"으로 보통 쓰입니다. 보통은 dfs 또는 bfs로 쓰일뿐이지 활용방법은 무궁무진합니다.
```
bool a[1004][1004];
for(int i = 0;i < V; i++){
for(int j = 0; j < V; j++){
if(a[i][j]){
bfs(i); 또는 dfs(i);
}
}
}
```
(아니 인프런.. 마크다운 된다며 진짜.. 하)
질문2. 인접리스트
A2. 아니요. 단방향 간선의 경우 하나만을 추가해야 합니다. 그러나 헷갈리지 않게 해당 부분 설명 추가했습니다.
Q. 3번노드로부터 5번 노드로 갈 수 있는 것을 어떻게 구현해야할까요?
adj[3].push_back(5);
앞의 코드는 3번에서 5번노드로 가는 단방향간선을 만든 것입니다.
만약 문제에서 3번에서 5번노드, 5번노드에서 3번노드로 가는 경로가 있다고 하면 다음 코드처럼 양방향 간선을 만들어야 합니다.
adj[3].push_back(5);
adj[5].push_back(3);
질문3. 시간복잡도
A3.
인접리스트는 인접행렬에 반해 자유분방한 그래프를 표현하기에 최적의 수단이고
>> 설명이 모호합니다. 자유분방한 그래프가 아니라 sparse한 그래프, dense한 그래프로 나뉘는데 sparse한 경우 인접리스트, dense한 경우 인접행렬이 좋습니다. / 해당 부분 설명 추가했어요. (블로그)
따라서 정점 V갯수가 많을 수록, 노드연결 갯수 E가 많을 수록 전체노드를 탐색하는 시간이 늘어난다고 이해했습니다.
>> 네 맞습니다.
또 질문 있으시면 언제든지 질문 부탁드립니다.
감사합니다.
강사 큰돌 올림.






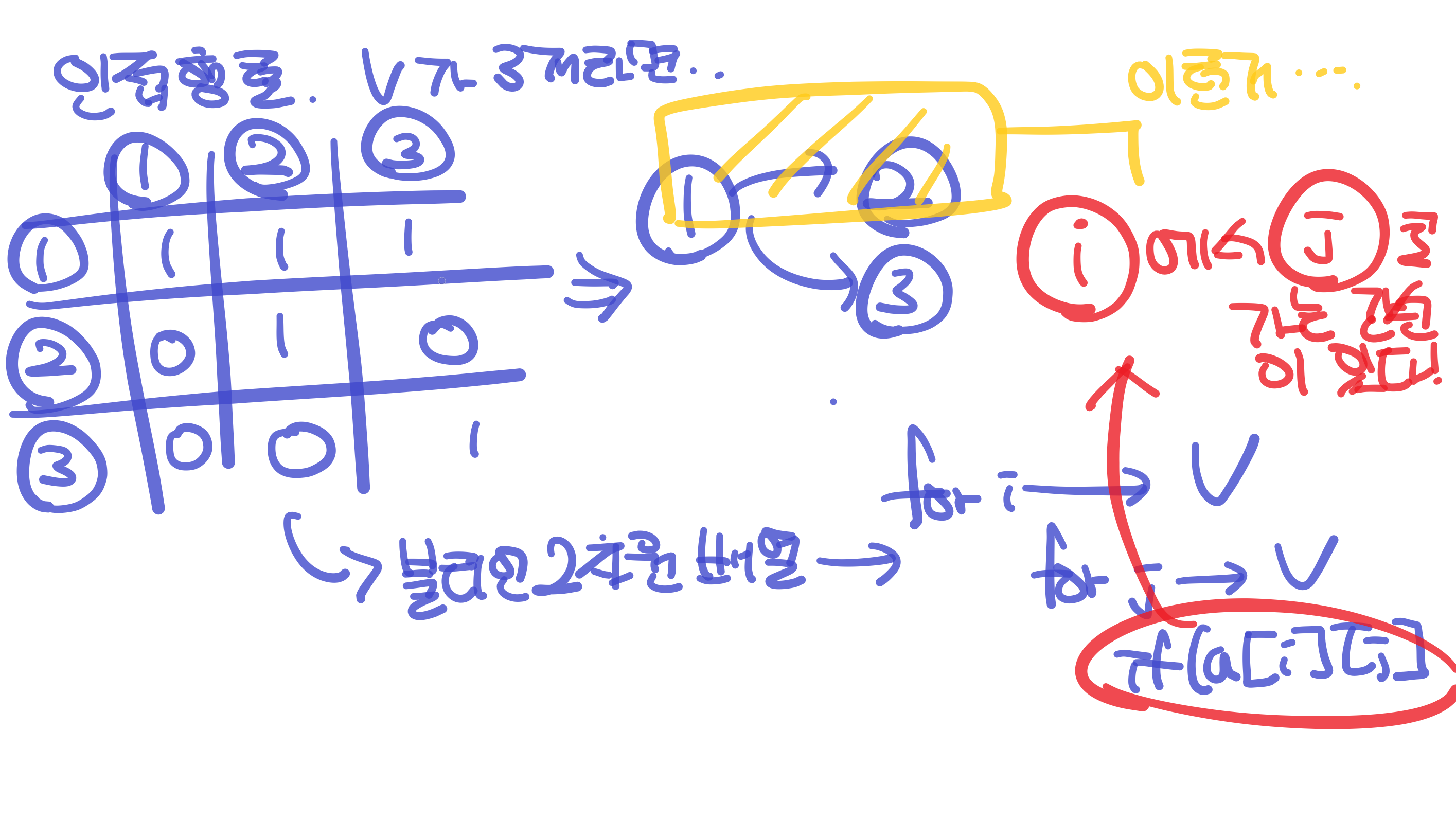
정확히 짚고 이해하고 싶어서 한 번 더 질문을 드리고싶습니다.
위 문제에서 주어진 지도의 크기는 가로 V, 세로V인 듯 합니다(이중 for문의 i, j크기로 유추)
(10 <= V <= 1000) 로 최대 범위를 가정할 수도 있겠고요.
질문. 위 문제에서 정점의 갯수가 V 인지과 정점의 갯수가 V*V 인지 물음에 대하여.
저는 V^2 개가 정답이라고 생각이드는데
선생님께서 주신 답변으로는 V개가 정답이라고 하신것 같아 아직도 구분을 못하고 있습니다 ㅠㅠ
다른 질문들은 해결됐습니다. 감사합니다.