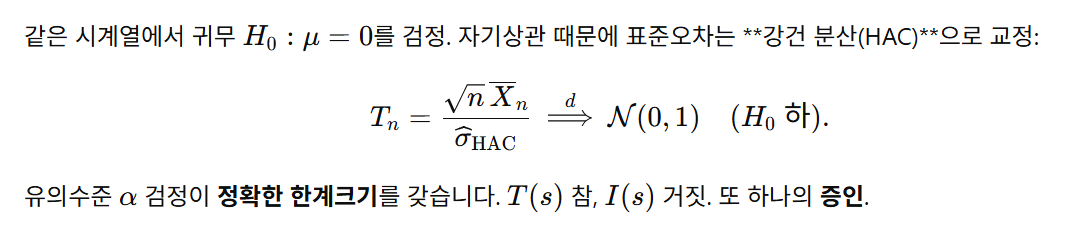
'독립이어야만 통계적으로 유의미하다'는 필요조건의 착각을 명제·술어논리로 반증하기

0. 독립적인 사건들이라야 통계적으로 의미가 있다.

많은 사람들이 이렇게 말합니다.
"자료가 독립적이어야만 통계가 의미가 있다."
"독립적이지 않다면 쓸모 없다."
결론부터 말하면 이러한 문장들은 거짓입니다. 독립성(independence)은 분석을 쉽게 만들어 주는 편리한 가정일 뿐, 추정·검정·예측의 타당성을 보장하는 필요조건은 아닙니다. 이 글은 그 주장을 명제논리와 술어논리로 형식화해 "필요조건이 아니다"가 정확히 무슨 뜻인지 구체적으로 보여 줍니다. 그리고 그 주장을 뒷받침하는 "증인(witness)" 사례도 제시합니다.

1. 논의의 준비: 기호와 뜻

원자 명제(참/거짓):

• I: "데이터(혹은 모형)에서 독립성이 성립한다."

• E: "선택한 절차가 타당한 추정을 제공한다."

• T: "선택한 절차가 유효한 검정을 제공한다." (설계된 유의수준 충족)

• P: "선택한 절차가 유효한 예측을 제공한다."

우리가 말하는 "통계적 의미"를

M  ≡  E ∨ T ∨ P

로 묶겠습니다. 즉, 추정·검정·예측 중 하나 이상이 제대로 작동한다는 뜻입니다.

2. 명제논리로 본 "필요조건이 아니다"

• "I가 M의 필요조건이다"의 형식은

  M ⇒ I.

  즉 M이면 반드시 I여야 한다.

• "필요조건이 아니다"는 위 명제의 부정입니다:

  ¬(M ⇒ I).

  고전 항등식 ¬(P ⇒ Q)≡P∧¬Q를 쓰면

   

   

  ¬(M ⇒ I) ≡ M∧¬I

  라는 결론이 나옵니다.

해석: "독립성은 필요조건이 아니다"란 말은,
'통계적 의미 M은 성립하지만 독립성 I은 깨지는' 상황이 하나라도 존재함을 뜻합니다.
필요조건 논쟁은 거창해 보이지만, 사실상 "반례 하나면 끝"이라는 말과 동치입니다.

같은 논리를 각 E,T,P에 적용하면

¬(E ⇒ I) ⁣  ⟺   ⁣E∧¬I, ¬(T ⇒ I) ⁣  ⟺   ⁣T∧¬I, ¬(P ⇒ I) ⁣  ⟺   ⁣P∧¬I.

즉 추정/검정/예측 각각에 대해 "독립성 없이도 된다"는 반례가 하나라도 있으면, 필요조건 주장은 무너집니다.

3. 술어논리(양화)와 집합론으로 본 정밀 해석

분석 세팅들의 집합을 S라 두고, 각 세팅 s∈S는
데이터 생성 메커니즘 D와 절차 Π의 쌍 s=(D,Π)라고 합시다.

술어:

• I(s): 세팅 s에서 독립성이 성립

• E(s),T(s),P(s): 각각 s에서 추정/검정/예측의 타당성

• M(s)≡E(s)∨T(s)∨P(s)M(s)
  
  그때

"I는 M의 필요조건"  ⟺  ∀s∈S,  M(s) ⇒ I(s).

따라서

  “필요조건이 아니다”  ⟺  ∃s*∈S: M(s*)∧¬I(s*)

입니다. 즉 단 하나의 증인 s* 만으로 결론이 납니다.

집합론 표기로는

I:={s:I(s)},M:={s:M(s)}.

필요조건   ⟺  M⊆I.
필요조건 아님   ⟺  M⊈I  ⟺  M∖I≠∅.

4. 증인(Witness) 제시: M∧¬I의 구체 사례

실제 통계에서 자주 등장하는 사례들을 짚어 보겠습니다.

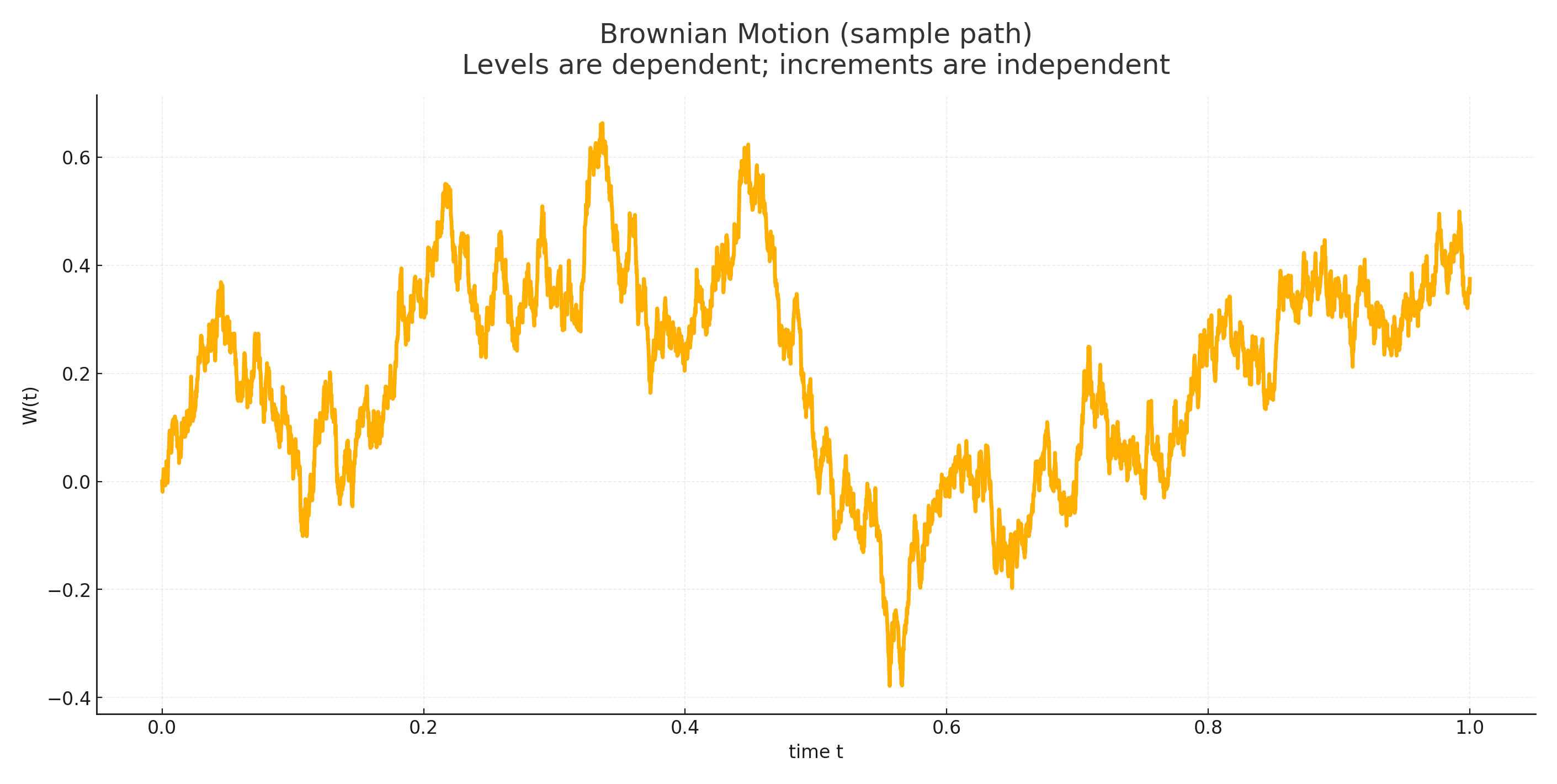
4.1 추정이 유효하지만 독립이 깨진다: 시계열(AR(1))

4.2 검정이 유효하지만 독립이 깨진다: HAC(뉴이–웨스트)

4.3 예측이 유효하지만 독립이 깨진다: 마르코프 체인

4.4 표본추출: 복원 없는 단순무작위추출(SRSWOR)

즉, 실제 통계에서 M∧¬I는 드문 예외가 아니라 전혀 아닙니다.

5. 흔한 오해와 정리

• 오해1: "독립이 아니면 통계가 다 망가진다."

• 답변: 망가지는 건 대개 독립을 전제한 분산 공식과 유의수준 계산입니다. 해결은 간단합니다. 의존 구조를 모델링하거나(시계열·공간·군집), 강건 분산(HAC, 군집화-강건, 블록부트스트랩 등)으로 교정하면 됩니다.

• 오해2: "그럼 독립은 쓸모없다?"

• 답변: 절대 그렇지 않습니다. 독립은 많은 교과서 공식과 정리를 단순화하는 강력한 충분조건입니다. 단지 필요조건은 아닙니다. 즉, 다른 조건들(혼합, 에르고딕성, 교환가능성, 마팅게일 차분 등)로도 M을 확보할 수 있다는 뜻입니다.

6. 논리식 요약

• 명제논리:
  “I는 M의 필요조건이 아니다”
    ⟺  ¬(M ⇒ I)  ⟺  M∧¬I (반례 하나면 충분)

• 술어논리:
  ∀s [M(s) ⇒ I(s)]가 거짓
    ⟺  ∃s* [M(s*)∧¬I(s*)] (증인의 존재)

• 집합론:
  M⊈I  ⟺  M∖I≠∅

8. 맺음말

독립성은 무적이 아닙니다. 논리의 언어로 말하면, 독립성은 M의 충분조건으로 자주 쓰이지만, 필요조건은 아닙니다. 그리고 그 사실은 M∧¬I인 증인의 존재로 간단하게 증명 할 수 있습니다.