인프런 워밍업 클럽 4기 CS 전공지식 1주차 발자국

2025-06-06T18:34:57.578Z

H_dong

강의 수강

나의 주력 언어는 c++이라서 강의를 토대로 c++버젼으로 바꿔보았다

이진 트리 BinaryTree.cpp

이진 트리의 주요 특징

각 노드는 왼쪽과 오른쪽 자식 노드를 최대 하나씩 가질 수 있습니다.
노드 수가 n일 때, 최대 높이는 n, 최소 높이는 log₂(n)입니다.
재귀적으로 구성되어 있어 왼쪽/오른쪽 서브트리도 이진 트리입니다.
트리 순회 방식에는 전위(preorder), 중위(inorder), 후위(postorder), 레벨 순서(level-order)가 있습니다.
노드의 위치가 중요하므로, 왼쪽 자식과 오른쪽 자식은 구분됩니다.

시간 복잡도 (BST 기준):

평균: 삽입, 탐색, 삭제 모두 O(log n)
최악: 트리가 한쪽으로 치우친 경우O(n)

#include <iostream>
using namespace std;

class BinaryTree {
private:
	struct Node {
		int data;
		Node* left;
		Node* right;

		Node(int data, Node* left = nullptr, Node* right = nullptr)
			: data(data), left(left), right(right) {}
	};

	Node* root;

public:
	BinaryTree(int data) {
		root = new Node(data);
	}
	
	~BinaryTree() {
		DestroyTree(root);
	}

	Node* GetRoot() const {
		return root;
	}

	Node* GetLeftSubTree() const {
		return root->left;
	}

	Node* GetRightSubTree() const {
		return root->right;
	}

	int getData() const {
		return root->data;
	}

	void printTree() const {
		printTree(root, 0);
	}

private:
	// 노드 탐색 (data 기준)
	Node* FindNode(Node* node, int data) 
	{
		if (node == nullptr) return nullptr;
		if (node->data == data) return node;

		Node* leftSearch = FindNode(node->left, data);
		if (leftSearch) return leftSearch;

		return FindNode(node->right, data);
	}

	// 트리 파괴
	void DestroyTree(Node* node)
	{
		if (node == nullptr) return;

		DestroyTree(node->left);
		DestroyTree(node->right);
		delete node;
	}

	// 전위 순회
	void PreOrderTraversal(Node* node) const
	{
		if (node == nullptr) return;
		cout << node->data << endl;
		PreOrderTraversal(node->left);
		PreOrderTraversal(node->right);
	}

	// 중위 순회
	void InOrderTraversal(Node* node) const
	{
		if (node == nullptr) return;
		InOrderTraversal(node->left);
		cout << node->data << endl;
		InOrderTraversal(node->right);
	}

	// 후위 순회
	void PostOrderTraversal(Node* node) const
	{
		if (node == nullptr) return;
		PostOrderTraversal(node->left);
		PostOrderTraversal(node->right);
		cout << node->data << endl;
	}

public:
	void SetLeftSubTree(BinaryTree* subtree)
	{
		root->left = subtree->root;
	}
	void SetLeftSubTree(int parentData, int data)
	{
		Node* parent = FindNode(root, parentData);
		if (parent) parent->left = new Node(data);
	}

	void SetRightSubTree(BinaryTree* subtree)
	{
		root->right = subtree->root;
	}
	void SetRightSubTree(int parentData, int data)
	{
		Node* parent = FindNode(root, parentData);
		if (parent) parent->right = new Node(data);
	}

	void PreOrderTraversal() const
	{
		PreOrderTraversal(root);
	}

	void InOrderTraversal() const
	{
		InOrderTraversal(root);
	}

	void PostOrderTraversal() const
	{
		PostOrderTraversal(root);
	}

	void printTree(Node* node, int depth) const {
		if (node == nullptr) return;

		// 우측 자식 먼저 출력 (트리의 오른쪽이 위로 가게)
		printTree(node->right, depth + 1);

		// 현재 노드 출력
		for (int i = 0; i < depth; ++i) cout << "    ";
		cout << node->data << endl;

		// 좌측 자식 출력
		printTree(node->left, depth + 1);
	}
};

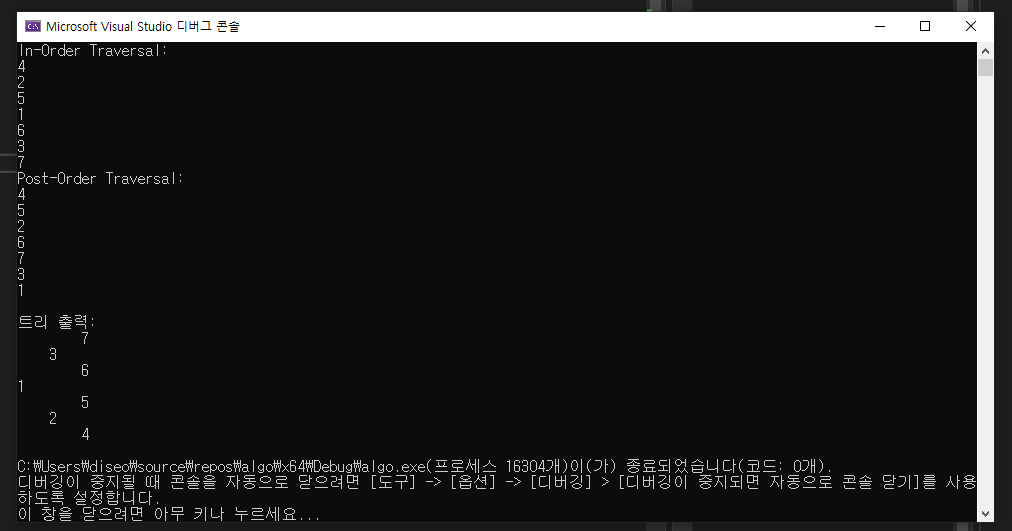
출력 결과

int main()
{
	BinaryTree tree(1);
	tree.SetLeftSubTree(1, 2);
	tree.SetRightSubTree(1, 3);
	tree.SetLeftSubTree(2, 4);
	tree.SetRightSubTree(2, 5);
	tree.SetLeftSubTree(3, 6);
	tree.SetRightSubTree(3, 7);

	cout << "Pre-Order Traversal: \n";
	tree.PreOrderTraversal();

	cout << "In-Order Traversal: \n";
	tree.InOrderTraversal();

	cout << "Post-Order Traversal: \n";
	tree.PostOrderTraversal();

	cout << "\n트리 출력:\n";
	tree.printTree();

	return 0;
}

이진 탐색 트리

BST의 주요 특징

왼쪽 서브트리에는 현재 노드보다 작은 값들,
오른쪽 서브트리에는 현재 노드보다 큰 값들이 위치합니다.
이 속성은 모든 하위 노드에서도 재귀적으로 적용됩니다.
중위 순회(Inorder Traversal)를 하면 오름차순 정렬된 값이 출력됩니다.
삽입, 삭제, 탐색 시 모두 이진 검색(Binary Search) 원리를 기반으로 진행됩니다.

시간 복잡도:

탐색, 삽입, 삭제 (평균): O(log n)
→ 트리가 균형 잡혀 있을 때 (ex: 높이가 log n 수준)
탐색, 삽입, 삭제 (최악): O(n)
→ 트리가 한쪽으로 치우친 경우 (ex: 정렬된 데이터만 삽입했을 때)

BST의 단점:

삽입 순서에 따라 트리 구조가 결정되므로, 균형이 무너지기 쉽습니다.
트리가 한쪽으로 치우치면 연결 리스트처럼 동작하게 되어 성능이 나빠집니다.
이를 보완하기 위해 AVL 트리, Red-Black 트리 같은 자가 균형 이진 탐색 트리가 존재합니다.

BinarySearchTree.h

#pragma once

enum class Color
{
	Red = 0,
	Black = 1,
};

struct Node
{
	Node* parent = nullptr;
	Node* left = nullptr;
	Node* right = nullptr;
	int key = {};
	Color color = Color::Black;
};
class BinarySearchTree
{
public:
	void Print() { Print(_root, 10, 0); }
	void Print(Node* node, int x, int y);

	void printTree() const { printTree(_root, 0); }
	void printTree(Node* node, int depth) const;

	Node* Search(Node* node, int key);
	Node* Search2(Node* node, int key);

	Node* Min(Node* node);
	Node* Max(Node* node);
	Node* Next(Node* node);

	void Insert(int key);
	void Delete(int key);
	void Delete(Node* node);
	void Replace(Node* u, Node* v);

private:
	Node* _root = nullptr;
};

BinarySearchTree.cpp

#include "BinarySearchTree.h"
#include <iostream>
#include <Windows.h>

using namespace std;

void SetCursorPosition(int x, int y)
{
	HANDLE output = ::GetStdHandle(STD_OUTPUT_HANDLE);
	COORD pos = { static_cast<SHORT>(x), static_cast<SHORT>(y) };
	::SetConsoleCursorPosition(output, pos);
}

void BinarySearchTree::Print(Node* node, int x, int y)
{
	if (node == nullptr)
		return;

	SetCursorPosition(x, y);

	cout << node->key;
	Print(node->left, x - (5 / (y + 1)), y + 1);
	Print(node->right, x + (5 / (y + 1)), y + 1);
}

void BinarySearchTree::printTree(Node* node, int depth) const
{
	if (node == nullptr) return;

	// 우측 자식 먼저 출력 (트리의 오른쪽이 위로 가게)
	printTree(node->right, depth + 1);

	// 현재 노드 출력
	for (int i = 0; i < depth; ++i) cout << "    ";
	cout << node->key << endl;

	// 좌측 자식 출력
	printTree(node->left, depth + 1);
}

Node* BinarySearchTree::Search(Node* node, int key)
{
	while (node && key != node->key)
	{
		if (key < node->key)
			node = node->left;
		else
			node = node->right;
	}

	return node;
}

Node* BinarySearchTree::Search2(Node* node, int key)
{
	if (node == nullptr || key == node->key)
		return node;

	if (key < node->key)
		return Search(node->left, key);
	else
		return Search(node->right, key);
}

Node* BinarySearchTree::Min(Node* node)
{
	while (node->left)
		node = node->left;

	return node;
}

Node* BinarySearchTree::Max(Node* node)
{
	while (node->right)
		node = node->right;

	return node;
}

Node* BinarySearchTree::Next(Node* node)
{
	if (node->right)
		return Min(node->right);

	Node* parent = node->parent;

	while (parent && node == parent->right)
	{
		node = parent;
		parent = parent->parent;
	}

	return parent;
}

void BinarySearchTree::Insert(int key)
{
	Node* newNode = new Node();
	newNode->key = key;

	if (_root == nullptr)
	{
		_root = newNode;
		return;
	}

	Node* node = _root;
	Node* parent = nullptr;

	while (node)
	{
		parent = node;
		if (key < node->key)
			node = node->left;
		else
			node = node->right;
	}

	newNode->parent = parent;

	if (key < parent->key)
		parent->left = newNode;
	else
		parent->right = newNode;
}

void BinarySearchTree::Delete(int key)
{
	Node* deleteNode = Search(_root, key);
	Delete(deleteNode);
}

void BinarySearchTree::Delete(Node* node)
{
	if (node == nullptr)
		return;

	if (node->left == nullptr)
		Replace(node, node->right);
	else if (node->right == nullptr)
		Replace(node, node->left);
	else
	{
		// 다음 데이터 찾기
		Node* next = Next(node);
		node->key = next->key;
		Delete(next);
	}
}

// u 서브트리를 v 서브트리로 교체
// 그리고 delete u
void BinarySearchTree::Replace(Node* u, Node* v)
{
	if (u->parent == nullptr)
		_root = v;
	else if (u == u->parent->left)
		u->parent->left = v;
	else
		u->parent->right = v;

	if (v)
		v->parent = u->parent;

	delete u;
}

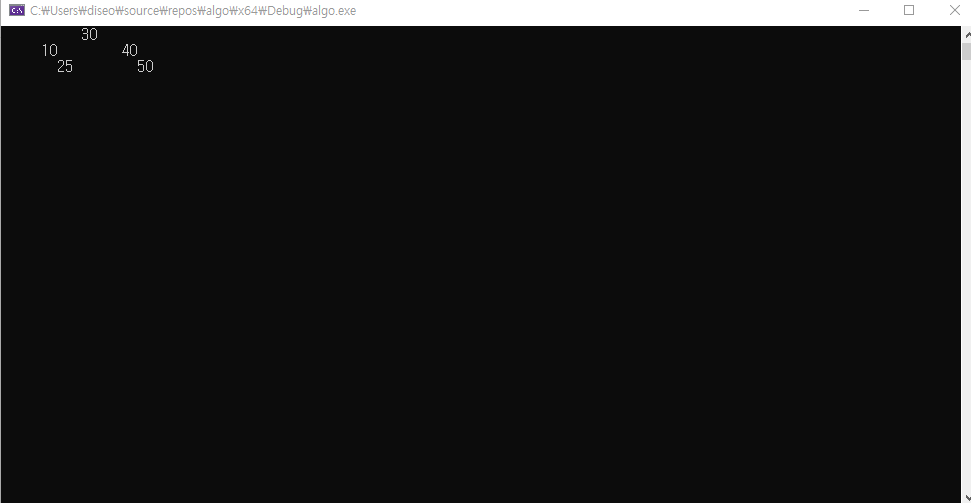
출력 결과

int main()
{
	BinarySearchTree bst;

	bst.Insert(30);
	bst.Insert(10);
	bst.Insert(20);
	bst.Insert(25);
	bst.Insert(26);
	bst.Insert(40);
	bst.Insert(50);

	bst.Delete(20);
	bst.Delete(26);

	bst.Print();
	system("pause");
}

AVL Tree

AVL 트리란?
AVL 트리는 높이 균형 이진 탐색 트리(Height-Balanced BST)의 일종으로, 모든 노드에서 왼쪽과 오른쪽 서브트리의 높이 차이가 1 이하가 되도록 균형을 유지하는 트리입니다. 1962년 Adelson-Velsky와 Landis가 고안했으며, 이름도 그들의 이니셜을 따왔습니다.

AVL 트리의 주요 특징

각 노드마다 균형 인자(Balance Factor)를 유지하며,
이는 왼쪽 서브트리 높이 - 오른쪽 서브트리 높이로 계산됩니다.
모든 노드의 균형 인자는 -1, 0, +1 중 하나여야 하며, 이를 벗어나면 회전을 통해 자동 복구합니다.
탐색, 삽입, 삭제 모두 O(log n) 시간에 수행되도록 보장합니다.
트리가 항상 균형을 유지하므로, 최악의 경우에도 성능이 안정적입니다.

AVL 트리의 장점

항상 트리의 높이가 O(log n)으로 제한되어 있어 탐색 성능이 매우 좋음
이진 탐색 트리의 최악의 경우(O(n))를 방지
정렬된 데이터를 입력해도 트리가 한쪽으로 치우치지 않음

AVL 트리의 단점

삽입과 삭제 시 회전 연산이 발생할 수 있어 구현이 복잡
삽입/삭제 연산이 많은 상황에서는 Red-Black Tree보다 오버헤드가 클 수 있음

AVL 트리는 언제 유용한가?

탐색 속도가 매우 중요한 시스템 (예: 데이터베이스 인덱스)
정렬된 데이터를 빈번하게 다루는 경우
트리의 높이가 항상 낮게 유지되어야 하는 실시간 시스템

AVLTree.h

#pragma once
#include <iostream>
class AVLTree
{
public:
	struct Node
	{
		Node* parent = nullptr;
		Node* left = nullptr;
		Node* right = nullptr;
		int key = {};
		int height = 1;
	};

public:
	void Print() { Print(_root, 10, 0); }
	void SetCursorPosition(int x, int y);
	void Print(Node* node, int x, int y);

	void printTree() const { printTree(_root, 0);
	std::cout << "--------------------------" << std::endl;
	}
	void printTree(Node* node, int depth) const;

	Node* Search(Node* node, int key);
	Node* Search2(Node* node, int key);

	Node* Min(Node* node);
	Node* Max(Node* node);
	Node* Next(Node* node);

	void Insert(int key);
	void Remove(int key);

	Node* GetRoot() { return _root; }

private:
	void UpdateHeight(Node* node);
	int GetHeight(Node* node);
	int GetBalance(Node* node);

	Node* RotateRight(Node* node);
	Node* RotateLeft(Node* node);

	Node* Rotate(Node* node, int key);
	Node* GetUnBalanceNode(Node* node);

	Node* Insert(Node* node, int key);
	Node* Remove(Node* node, int key);
	Node* RemoveHelper(Node* node);

	Node* _root = nullptr;
};

AVLTree.cpp

#include "AVLTree.h"
#include <iostream>
#include <Windows.h>

using namespace std;

void AVLTree::SetCursorPosition(int x, int y)
{
	HANDLE output = ::GetStdHandle(STD_OUTPUT_HANDLE);
	COORD pos = { static_cast<SHORT>(x), static_cast<SHORT>(y) };
	::SetConsoleCursorPosition(output, pos);
}

void AVLTree::Print(Node* node, int x, int y)
{
	if (node == nullptr)
		return;

	SetCursorPosition(x, y);

	cout << node->key;
	Print(node->left, x - (5 / (y + 1)), y + 1);
	Print(node->right, x + (5 / (y + 1)), y + 1);
}

void AVLTree::printTree(Node* node, int depth) const
{
	if (node == nullptr) return;

	// 우측 자식 먼저 출력 (트리의 오른쪽이 위로 가게)
	printTree(node->right, depth + 1);

	// 현재 노드 출력
	for (int i = 0; i < depth; ++i) cout << "    ";
	cout << node->key << endl;

	// 좌측 자식 출력
	printTree(node->left, depth + 1);
}

AVLTree::Node* AVLTree::Search(Node* node, int key)
{
	while (node && key != node->key)
	{
		if (key < node->key)
			node = node->left;
		else
			node = node->right;
	}

	return node;
}

AVLTree::Node* AVLTree::Search2(Node* node, int key)
{
	if (node == nullptr || key == node->key)
		return node;

	if (key < node->key)
		return Search(node->left, key);
	else
		return Search(node->right, key);
}

AVLTree::Node* AVLTree::Min(Node* node)
{
	while (node->left)
		node = node->left;

	return node;
}

AVLTree::Node* AVLTree::Max(Node* node)
{
	while (node->right)
		node = node->right;

	return node;
}

AVLTree::Node* AVLTree::Next(Node* node)
{
	if (node->right)
		return Min(node->right);

	Node* parent = node->parent;

	while (parent && node == parent->right)
	{
		node = parent;
		parent = parent->parent;
	}

	return parent;
}



void AVLTree::UpdateHeight(Node* node)
{
	int lh = GetHeight(node->left);
	int rh = GetHeight(node->right);
	node->height = max(lh, rh) + 1;
}

int AVLTree::GetHeight(Node* node)
{
	return node ? node->height : 0;
}

int AVLTree::GetBalance(Node* node)
{
	return node ? GetHeight(node->left) - GetHeight(node->right) : 0;
}

//		[childNode]
//	[node]			[3]
// [1] [2]

//		[node]
//	[1]		[childNode]
//			[2]		[3]
AVLTree::Node* AVLTree::RotateRight(Node* node)
{
	Node* childNode = node->left;

	node->left = childNode->right;

	if (childNode->right != nullptr)
		childNode->right->parent = node;

	childNode->parent = node->parent;

	if (node->parent == nullptr)
		_root = childNode;
	else if (node == node->parent->right)
		node->parent->right = childNode;
	else
		node->parent->left = childNode;

	childNode->right = node;
	node->parent = childNode;

	UpdateHeight(node);
	UpdateHeight(childNode);

	return childNode;
}

AVLTree::Node* AVLTree::RotateLeft(Node* node)
{
	Node* childNode = node->right;

	node->right = childNode->left;

	if (childNode->left != nullptr) 
		childNode->left->parent = node;

	childNode->parent = node->parent;

	if (node->parent == nullptr)
		_root = childNode;
	else if (node == node->parent->left)
		node->parent->left = childNode;
	else
		node->parent->right = childNode;

	childNode->left = node;
	node->parent = childNode;

	UpdateHeight(node);
	UpdateHeight(childNode);

	return childNode;
}

AVLTree::Node* AVLTree::Rotate(Node* targetNode, int data)
{
	int balance = GetBalance(targetNode);
	bool isRootNode = false;
	if (targetNode == _root)
		isRootNode = true;

	if (balance < -1 && data > targetNode->right->key)	  // LL
	{
		targetNode = RotateLeft(targetNode);
	}
	else if (balance > 1 && data < targetNode->left->key) // RR
	{
		targetNode = RotateRight(targetNode);
	}
	else if (balance > 1 && data > targetNode->left->key) // LR
	{
		targetNode->left = RotateLeft(targetNode->left);
		targetNode = RotateRight(targetNode);
	}
	else if (balance < -1 && data < targetNode->right->key) // RL
	{
		targetNode->right = RotateRight(targetNode->right);
		targetNode = RotateLeft(targetNode);
	}

	if (isRootNode)
	{
		_root = targetNode;
	}

	return targetNode;
}

AVLTree::Node* AVLTree::GetUnBalanceNode(Node* node) {
	if (!node) return nullptr;
	int balance = GetBalance(node);
	if (balance > 1 || balance < -1)
		return node;
	return nullptr;
}


void AVLTree::Insert(int key)
{
	_root = Insert(_root, key);
}

AVLTree::Node* AVLTree::Insert(Node* node, int key)
{
	if (!node) return new Node{ nullptr, nullptr, nullptr, key, 1 };
	if (key < node->key) 
	{
		node->left = Insert(node->left, key);
		if (node->left) node->left->parent = node;
	}
	else if (key > node->key)
	{
		node->right = Insert(node->right, key);
		if (node->right) node->right->parent = node;
	}
	else
	{
		return node;
	}
	
	UpdateHeight(node);
	return Rotate(node, key);
}

void AVLTree::Remove(int key)
{
	_root = Remove(_root, key);
}

AVLTree::Node* AVLTree::Remove(Node* node, int key)
{
	if (!node) return nullptr;

	if (key == 5)
		int a = 0;
	if (key < node->key)
	{
		node->left = Remove(node->left, key);
	}
	else if (key > node->key)
	{
		node->right = Remove(node->right, key);
	}
	else
	{
		node = RemoveHelper(node);
	}
	if (!node) return nullptr;

	UpdateHeight(node);
	Node* unbalanced = GetUnBalanceNode(node);
	if (unbalanced)
		return Rotate(unbalanced, key);
	return node;
}

AVLTree::Node* AVLTree::RemoveHelper(Node* node)
{
	if (!node->left || !node->right) // 자식 노드가 하나 이하일 경우
	{
		Node* temp = node->left ? node->left : node->right;
		if (!temp)
		{
			// 자식이 아예 없는 경우
			delete node;
			return nullptr;
		}
		else
		{
			// 자식이 하나 있는 경우 -> 그 자식으로 자신을 대체
			*node = *temp;
			delete temp;
			return node;
		}
	}
	else
	{
		// 자식이 둘 다 있는 경우
		Node* temp = Min(node->right); // 오른쪽 서브트리에서 가장 작은 값 (후계자)
		node->key = temp->key;
		node->right = Remove(node->right, temp->key);
		return node;
	}
}

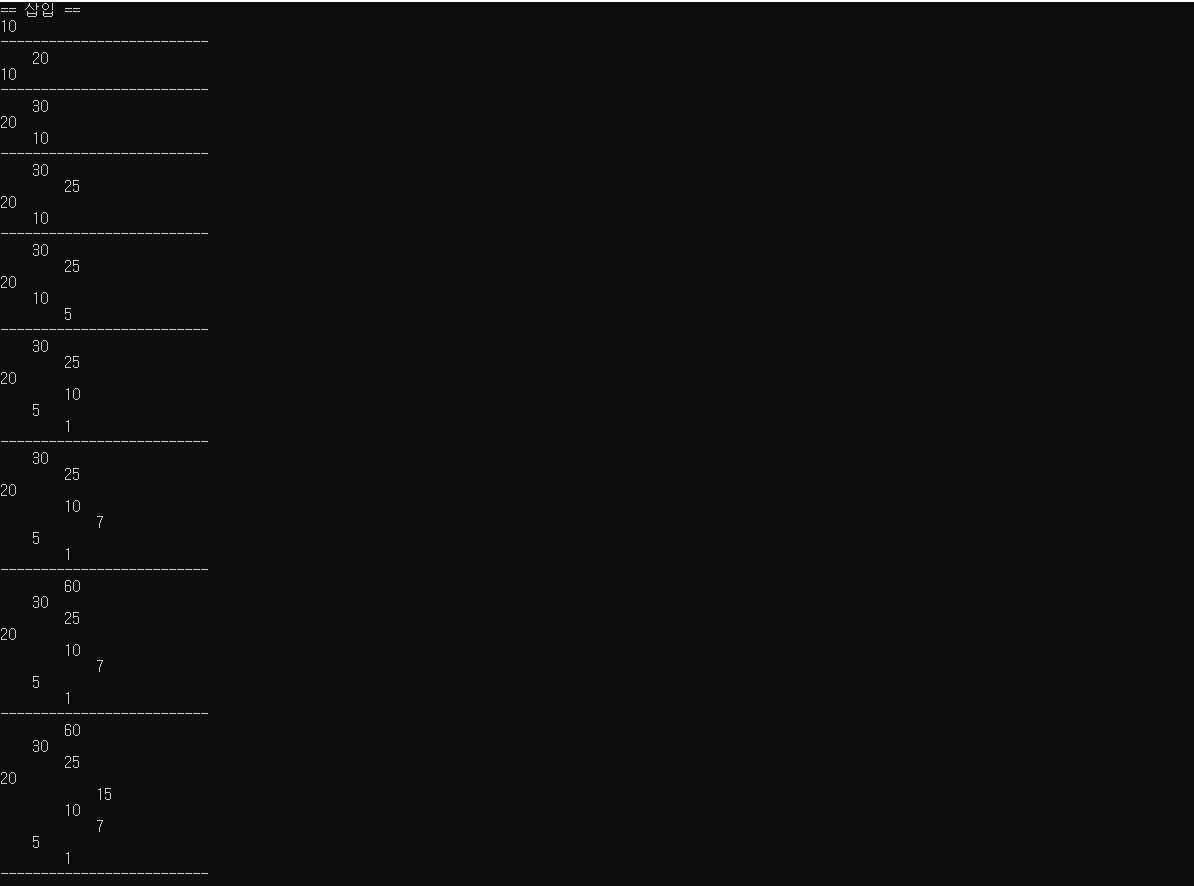
출력 결과

int main() {
	AVLTree tree;

	cout << "== 삽입 ==" << endl;
	tree.Insert(10);
	tree.printTree();
	tree.Insert(20);
	tree.printTree();
	tree.Insert(30);
	tree.printTree();
	tree.Insert(25);
	tree.printTree();
	tree.Insert(5);
	tree.printTree();
	tree.Insert(1);
	tree.printTree();
	tree.Insert(7);
	tree.printTree();
	tree.Insert(60);
	tree.printTree();
	tree.Insert(15);
	tree.printTree();

	cout << endl;

	cout << "== 삭제 ==" << endl;
	tree.Remove(30); // 자식 2개 있는 노드 삭제
	tree.Remove(10); // 루트 노드 삭제
	tree.Remove(1);  // 리프 노드 삭제

	tree.printTree();
	cout << endl;

	return 0;
}

알고리즘 · 자료구조 자료구조 알고리즘 워밍업클럽4기 CS전공지식

답변 0