들어가며

• 일단 만나본 투포인터 유형들에 대해서 코드가 간단하게 나오는 경우가 많아서 공유하고자 합니다.

  • 참고: 몇 문제 풀어보지 않아서 공유하는 코드를 응용해야 하는 경우도 있을 것 같습니다.

유형

• 제가 확인했던 투포인터 유형의 경우 다음 공통점이 특징적이었습니다.

  • 어떤 수열이 있고, 그 수열의 연속된 구간 각각에 대해서 어떤 값을 도출해낼 수 있다.

  • 한 구간이 다른 구간을 완전하게 포함하고 있으면 도출해낸 값도 더 커진다.

  • 도출값이 정확히 X가 되는 경우 or X 이상인 도출값들 중 최소값을 구한다.

예시 문제 풀이

• a = [1, 2, 3]의 연속한 구간의 합들 중 1.5보다 큰 값들 중 최소값을 구하는 문제를 풀어보겠습니다.

  • 연속한 구간의 시작과 끝 인덱스를 i와 j로 놓고 (a[i]는 구간에 포함, a[j]는 미포함) 전체 과정을 그림으로 나타내면 다음과 같습니다.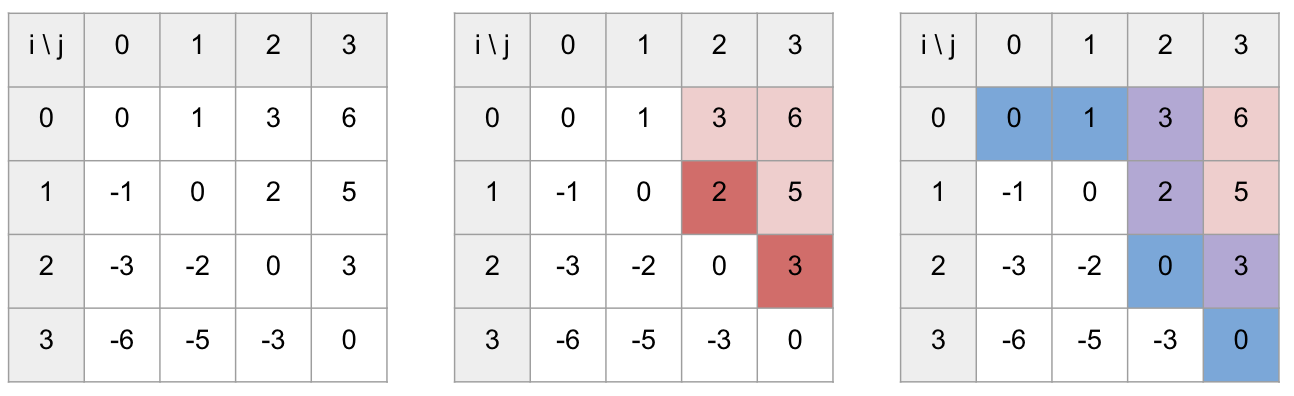
    

    • 첫 번째 표는 모든 i와 j에 대해서 합을 구한 모습입니다.

      • 이 문제에서는 i가 j보다 큰 경우는 고려할 필요가 없지만 그 경우에도 이 알고리즘이 잘 작동한다는 것을 보여주기 위해서, i가 j보다 큰 경우 부분합을 음수로 계산한다고 가정하고 넣었습니다.

      • 여기서 눈여겨볼점은 값이 i가 증가할수록 작아지고, j가 증가할수록 커진다는 점입니다.

        • 직관적으로 오른쪽이나 위로 갈수록 숫자가 커진다고 볼 수도 있습니다.

    • 두 번째 표는 합들 중 1.5보다 크거나 같은 영역을 붉은색으로 색칠한 것입니다.

      • 이 때 어떤 칸이 색칠되어 있으면, 그 칸보다 오른쪽이나 위에 있는 칸들은 1.5보다 크기 때문에 그 칸의 오른쪽 위의 영역들이 모두 붉은색으로 색칠된 것을 볼 수 있습니다.

      • 이 때 문제에서 1.5보다 큰 값들 중 최소값을 구하려면 색칠된 칸들 중 가장 왼쪽 아래에 있는 값들만 고려하면 된다는 것을 확인할 수 있습니다. 진한 붉은 색으로 나타냈습니다.

    • 세 번째 표는 알고리즘의 진행을 나타냅니다.

      • 합이 1.5보다 작으면 오른쪽으로 진행하고, 합이 1.5 이상이면 아래쪽으로 진행합니다.

      • 진행한 칸을 파란색으로, 붉은 영역과 겹치는 칸들은 보라색으로 나타냈습니다.

        • 아래 소개드릴 코드는 보라색 칸들에 대해서 원하는 로직을 실행하게 됩니다.

      • 붉은 영역을 여러 개 가지고 실험해보시면, 이렇게 진행할 경우 붉은 영역의 아래 경계를 훑고 지나간다는 것을 확인할 수 있습니다. 따라서 보라색 칸들이 위에서 언급한 가장 왼쪽 아래 칸들을 포함한다는 것을 알 수 있습니다.

         

코드

• 제가 현재 사용하고 있는 코드는 다음과 같습니다.

  function* solve(f, lowerBound, iMax, jMax) {
      let [i, j] = [0, 0]
      while (i <= iMax && j <= jMax) {
          if (f(i, j) >= lowerBound) {
              yield f(i, j)
              ++i
          } else {
              ++j
          }
      }
  }
  
  function main() {
      // ...
      const candidates = [...solve(f, lowerBound, iMax, jMax)]
      const result = Math.min(...candidates)
  }

• 구간의 합 특수 경우: 투포인터 문제의 경우 f 함수로 구간의 합을 구하는 경우가 대표적인데, 아쉽게도 위 코드와 f = (i, j) => nums.slice(i, j).reduce((a, b) => a + b, 0)으로 구현 시 구간합을 구하는 데만 시간복잡도 최대 O(n), 총 O(n^2)로 시간초과가 나는 경우가 있습니다.

  • 따라서 구간의 합을 O(1)안에 구해주기 위해서 다음과 같이 sum이라는 변수에 합을 저장하고, 이전의 합을 이용해 인덱스 업데이트 시 합도 같이 업데이트해주는 방식을 사용하면 전체 시간복잡도 O(n) 안에 해결할 수 있습니다.

    function* solve(xs, lowerBound, iMax, jMax) {
        let [i, j, sum] = [0, 0, 0]
        while (i <= iMax && j <= jMax) {
            if (sum >= lowerBound) {
                yield sum
                ;[i, sum] = [i + 1, sum - xs[i]]
            } else {
                ;[j, sum] = [j + 1, sum + xs[j]]
            }
        }
    }

  • 참고: i와 sum과 같이 여러 값들을 한 번에 업데이트할 때 업데이트 순서에 따른 버그를 방지하기 위해서 저는 JS의 구조 분해 할당 문법을 애용하고 있습니다.

주의사항

• iMax와 jMax가 문제에 따라 length가 될 수도 있고 length + 1이 될 수도 있습니다.