컴퓨터 구조

✅ 프로그램 실행 구조

PC (Program Counter): 다음 명령어 주소를 저장하는 레지스터
SP (Stack Pointer): 함수 호출, 지역 변수 관리를 위한 스택 위치 추적
Fetch-Execute 사이클:
- 명령어 인출 (PC → 메모리)
- 명령어 실행 (ALU, 메모리 접근, 분기 등)

✅ 명령어 종류 요약

NOP: 아무 작업 안 함
LOADA: 메모리 → A 레지스터
LOADI: 상수 → A 레지스터
STOREA: A 레지스터 → 메모리
ADD: 덧셈
SUB: 뺄셈
OUT: A 레지스터 출력
HLT: 프로그램 종료

✅ 분기 명령어

JMP addr: 무조건 점프
JMPC: Carry 플래그가 1일 때 점프
JMPZ: Zero 플래그가 1일 때 점프

✅ 제어 장치/출력 구성

출력 레지스터: 출력 대기 중인 데이터를 저장
제어 장치: 명령어 해석 → ALU, 레지스터, 메모리 제어 신호 생성

✅ 기계어 vs 어셈블리어

기계어: 2진수 코드 (01101001)
어셈블리어: 사람 친화적 언어 (LOAD, ADD)
어셈블러: 어셈블리어 → 기계어로 번역

자료구조와 알고리즘

✅ Trie란?

문자열 검색/자동완성에 특화된 트리 형태의 자료구조

✅ 핵심 개념

각 노드는 문자 하나를 표현
루트부터 자식 노드들을 따라가며 문자열을 구성
한 노드에서 다음 노드로 이동할 때 문자 하나씩 비교

✅ 특징 요약

자료구조 : 형태다진 트리 (보통 26개 자식 노드: 알파벳 a~z)

저장 단위 : 문자열 전체가 아닌, 문자 하나씩 저장

검색 속도 : O(문자열 길이) (문자 수만큼 비교)

공간 사용량 : 중복 접두사를 공유하므로 공간 효율적

사용 용도 : 자동완성, 사전 검색, 접두어 필터링 등

✅ 장점

검색과 삽입이 O(L) (L = 문자열 길이)
공통 접두어 공유로 공간 절약
자동완성, 필터링, 문자열 집합 처리에 탁월

✅ 단점

구현이 복잡할 수 있음
알파벳 수가 많으면 공간 낭비 가능 (자식 노드 많음)

Trie

#pragma once
#include <unordered_map>
#include <string>

using namespace std;

class TrieNode
{
public:
	unordered_map<char, TrieNode*> children;
	bool isEndOfWord = false;
};

class Trie
{
public:
	Trie();
	~Trie();

	void Insert(const string& word);
	bool Search(const string& word);

	vector<string> Autocomplete(const string& prefix);

private:
	void Dfs(TrieNode* node, const string& path, vector<string>& results);

	TrieNode* _root;

};

#include "Trie.h"
#include <iostream>
#include <unordered_map>
#include <vector>
#include <string>

Trie::Trie()
{
	_root = new TrieNode();
}

Trie::~Trie()
{
	delete _root;
}

void Trie::Insert(const string& word)
{
	TrieNode* node = _root; // 루트에서 시작
	for (char c : word)
	{
		if (!node->children.count(c))
			node->children[c] = new TrieNode(); // 해당 문자 노드가 없으면 생성
		
		node = node->children[c]; // 다음 글자로 이동
	}
	node->isEndOfWord = true; // 마지막 글자에서 단어 종료 표시
}

bool Trie::Search(const string& word)
{
	TrieNode* node = _root; // 루트에서 시작
	for (char c : word)
	{
		if (!node->children.count(c))
			return false;

		node = node->children[c]; // 다음 글자로 이동
	}

	return node->isEndOfWord;
}

// 사용자가 입력한 접두어로 시작하는 모든 단어를 찾아 반환하는 함수
vector<string> Trie::Autocomplete(const string& prefix)
{
	vector<string> results;

	TrieNode* node = _root;
	for (char c : prefix)
	{
		// 중간에 접두어에 해당하는 경로가 없으면, 자동완성 결과도 없음 (빈 벡터 반환)
		if (!node->children.count(c)) 
			return results;
		
		node = node->children[c];
	}
	// 접두어의 마지막 노드까지 도달한 후, 거기서부터 모든 하위 단어를 Dfs로 찾음
	Dfs(node, prefix, results);
	return results;
}

// 현재 노드부터 시작해서 하위 모든 단어를 탐색하고, 완성된 단어를 results에 저장
// 이로써 "ap" -> "apple", "april", "app" 등 다양한 자동완성 결과 생성
void Trie::Dfs(TrieNode* node, const string& path, vector<string>& results)
{
	// 지금까지의 경로가 하나의 완성된 단어라면 results에 추가
	if (node->isEndOfWord)
	{
		results.push_back(path);
	}
	for (auto& [c, nextNode] : node->children)
	{
		// 각각의 자식 문자 붙여서 자식 호출
		Dfs(nextNode, path + c, results);
	}
}

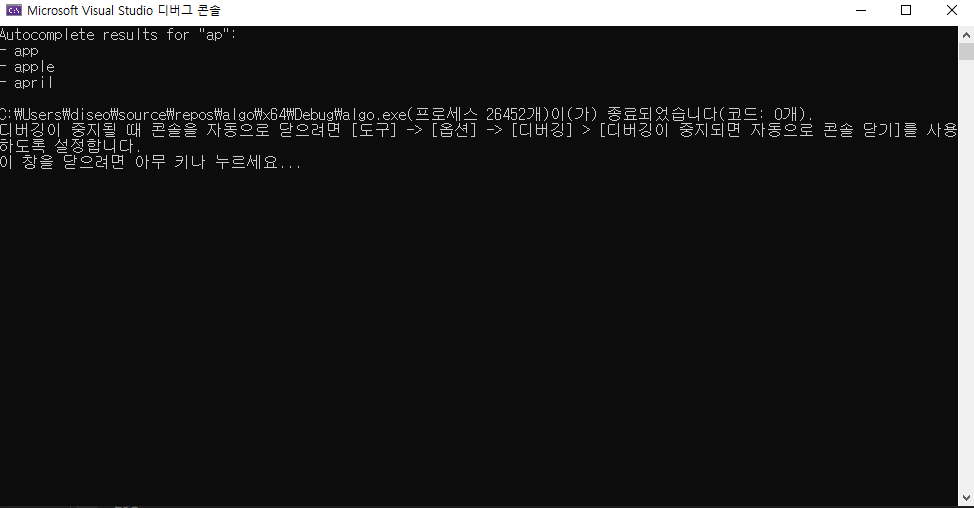
출력 결과

int main()
{
	Trie trie;
	trie.Insert("apple");
	trie.Insert("app");
	trie.Insert("april");
	trie.Insert("bat");
	trie.Insert("ball");

	string prefix = "ap";
	vector<string> suggestions = trie.Autocomplete(prefix);

	cout << "Autocomplete results for \"" << prefix << "\":\n";
	for (const string& word : suggestions) {
		cout << "- " << word << endl;
	}

	return 0;
}

✅ 그래프(Graph)란?

- 정점(Vertex)과 간선(Edge)으로 이루어진 자료구조

- 정점끼리의 연결 관계를 표현

- 방향성, 가중치, 연결 여부 등에 따라 다양하게 분류됨

✅ DFS (깊이 우선 탐색)

- 한 방향으로 계속 깊이 들어가며 탐색

- 스택(Stack) 또는 재귀(Recursion) 사용

- 방문 → 깊이 탐색 → 백트래킹

- 미로 찾기, 백트래킹 등에 적합

- 시간복잡도: O(V + E)

✅ BFS (너비 우선 탐색)

- 현재 노드의 인접 노드를 모두 방문 후 다음 단계로 진행

- 큐(Queue) 사용

- 최단 거리 문제에 유리 (간선 가중치 동일할 때)

- 시간복잡도: O(V + E)

✅ DFS vs BFS 요약 비교

항목 : DFS | BFS

--------:----------------------------|-------------------------------

방식 : 깊이 우선 (한 방향으로 쭉) | 너비 우선 (레벨 순으로)

자료구조 : 스택 / 재귀 | 큐

특징 : 백트래킹, 경로 탐색 적합 | 최단 거리 탐색에 적합

시간복잡도: O(V + E) | O(V + E)

DFS

#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
#include <unordered_set>

using namespace std;

class DFS
{
	struct Vertex
	{
		string data;
	};

public:
	void CreateGraph()
	{
		vertices.resize(8);

		vertices =
		{
			{"Ben"}, {"Ivy"}, {"Joy"}, {"Jake"},
			{"Anna"}, {"David"}, {"Elin"}, {"Owen"}
		};

		// 인접 리스트
		adjacent["Ben"] = { "Ivy", "Jake", "Anna", "David" };
		adjacent["Ivy"] = { "Ben", "Joy" };
		adjacent["Joy"] = { "Ivy", "Jake" };
		adjacent["Jake"] = { "Ben", "Joy" };
		adjacent["Anna"] = { "Ben" };
		adjacent["David"] = { "Ben", "Elin" };
		adjacent["Elin"] = { "David", "Owen" };
		adjacent["Owen"] = { "Elin" };

	}

	void Dfs(const string& here)
	{
		// 방문
		visited.insert(here);
		cout << "Visited : " << here << endl;

		for (const string& there : adjacent[here])
		{
			if (visited.count(there) == 0)
				Dfs(there);
		}
	}

	void DfsAll()
	{
		visited.clear();

		for (const Vertex& v : vertices)
		{
			if (visited.count(v.data) == 0)
				Dfs(v.data);
		}


	}

private:
	vector<Vertex> vertices;
	unordered_map<string, vector<string>> adjacent;
	unordered_set<string> visited;
};

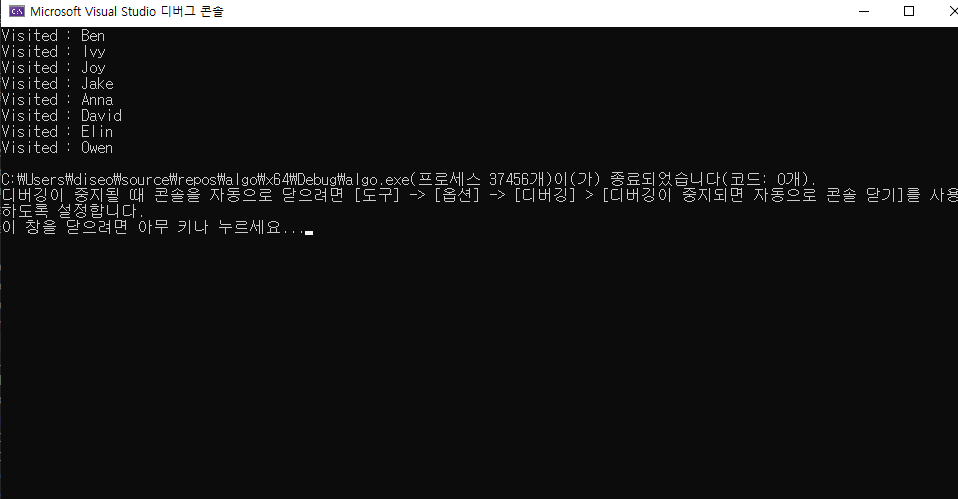
출력 결과

int main() 
{
	DFS d;

	d.CreateGraph();
	d.DfsAll();
	return 0;
}

BFS

#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
#include <unordered_set>

using namespace std;

class BFS
{
	struct Vertex
	{
		string data;
	};

public:
	void CreateGraph()
	{
		vertices.resize(8);

		vertices =
		{
			{"Ben"}, {"Ivy"}, {"Joy"}, {"Jake"},
			{"Anna"}, {"David"}, {"Elin"}, {"Owen"}
		};

		// 인접 리스트
		adjacent["Ben"] = { "Ivy", "Jake", "Anna", "David" };
		adjacent["Ivy"] = { "Ben", "Joy" };
		adjacent["Joy"] = { "Ivy", "Jake" };
		adjacent["Jake"] = { "Ben", "Joy" };
		adjacent["Anna"] = { "Ben" };
		adjacent["David"] = { "Ben", "Elin" };
		adjacent["Elin"] = { "David", "Owen" };
		adjacent["Owen"] = { "Elin" };

	}

	void Bfs(string here)
	{
		// 누구에 의해 발견 되었는지?
		unordered_map<string, string> parent;
		// 시작점에서 얼만큼 떨어져 있는지?
		unordered_map<string, int> distance;

		queue<string> q;
		q.push(here);
		discovered.insert(here);

		parent[here] = here;
		distance[here] = 0;

		while (q.empty() == false)
		{
			here = q.front();
			q.pop();

			cout << "Visited : " << here << endl;

			for (string there : adjacent[here])
			{
				if (discovered.count(there) != 0)
					continue;

				q.push(there);
				discovered.insert(there);

				parent[there] = here;
				distance[there] = distance[here] + 1;
			}
		}
	}

	void BfsAll()
	{
		for (Vertex v : vertices)
		{
			if (discovered.count(v.data) == 0)
				Bfs(v.data);
		}

	}

private:
	vector<Vertex> vertices;
	unordered_map<string, vector<string>> adjacent;
	unordered_set<string> discovered;
};

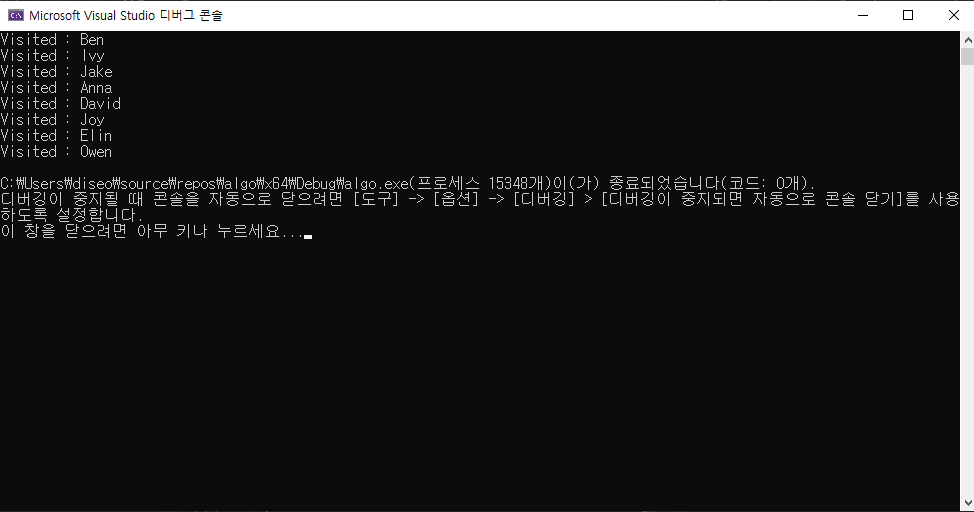
출력 결과

int main()
{
	BFS b;

	b.CreateGraph();
	b.BfsAll();
	return 0;
}

✅ 다익스트라 알고리즘이란?

하나의 시작 정점에서 다른 모든 정점까지의 최단 거리를 구하는 알고리즘
(단, 모든 간선 가중치는 0 이상이어야 함)

✅ 핵심 개념

방문하지 않은 정점 중에서 가장 가까운 정점을 반복적으로 선택
선택된 정점의 인접 정점 거리들을 갱신
우선순위 큐(Min Heap)를 사용하면 성능을 높일 수 있음
거리 배열과 방문 배열을 함께 사용

✅ 특징 요약

알고리즘 유형 : 그리디 알고리즘 (Greedy)
그래프 조건 : 방향/무방향 그래프 + 양의 가중치
시간 복잡도 : O(E log V) (우선순위 큐 + 인접 리스트 사용 시)
자료구조 : 거리 배열, 우선순위 큐, 방문 여부 배열
적용 분야 : GPS, 게임 경로 탐색, 네트워크 최단 경로 등

✅ 장점

모든 정점까지의 최단 거리를 빠르게 구할 수 있음
우선순위 큐와 함께 사용하면 성능이 우수
실제 현실 문제에 널리 사용됨 (지도, 경로 탐색 등)

✅ 단점

음수 가중치가 있는 그래프에서는 동작하지 않음
경로가 아닌 거리 정보만 기본 출력됨 (경로 추적은 따로 저장해야 함)
단순 구현(O(V²))은 느릴 수 있음 (우선순위 큐 사용 필요)

Dijkstra

#include <iostream>
#include <vector>
#include <queue>
#include <string>
#include <stack>

using namespace std;

class DIJKSTRA
{
	struct Vertex
	{
		string name;
		int cost = INT32_MAX;
	};

public:
	vector<Vertex> vertices;
	vector<vector<int>> adjacent;

	void CreateGraph()
	{
        vertices = 
        {
            {"서울"}, {"원주"}, {"강릉"}, 
            {"대전"}, {"전주"}, {"대구"}
        };

        adjacent = vector<vector<int>>(6, vector<int>(6, -1));

        adjacent[0][1] = 87;
        adjacent[0][2] = 165;
        adjacent[0][3] = 140;
        adjacent[0][4] = 187;

        adjacent[1][0] = 87;
        adjacent[1][2] = 95;
        adjacent[1][3] = 118;
        adjacent[1][5] = 178;

        adjacent[2][0] = 165;
        adjacent[2][1] = 95;
        adjacent[2][5] = 212;

        adjacent[3][0] = 140;
        adjacent[3][1] = 118;
        adjacent[3][4] = 56;
        adjacent[3][5] = 122;

        adjacent[4][0] = 187;
        adjacent[4][3] = 56;
        adjacent[4][5] = 130;

        adjacent[5][1] = 178;
        adjacent[5][2] = 212;
        adjacent[5][3] = 122;
        adjacent[5][4] = 130;
	}

    void Dijkstra(int here)
    {
        vector<int> parent(6, -1);
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq; // cost, vertex

        vertices[here].cost = 0;
        parent[here] = here;
        pq.push({ 0, here });

        while (!pq.empty())
        {
            auto [cost, here] = pq.top();
            pq.pop();

            if (vertices[here].cost < cost)
                continue;

            for (int there = 0; there < 6; ++there)
            {
                if (adjacent[here][there] == -1)
                    continue;

                int nextCost = vertices[here].cost + adjacent[here][there];
                if (nextCost < vertices[there].cost)
                {
                    vertices[there].cost = nextCost;
                    parent[there] = here;
                    pq.push({ nextCost, there });
                }
            }
        }

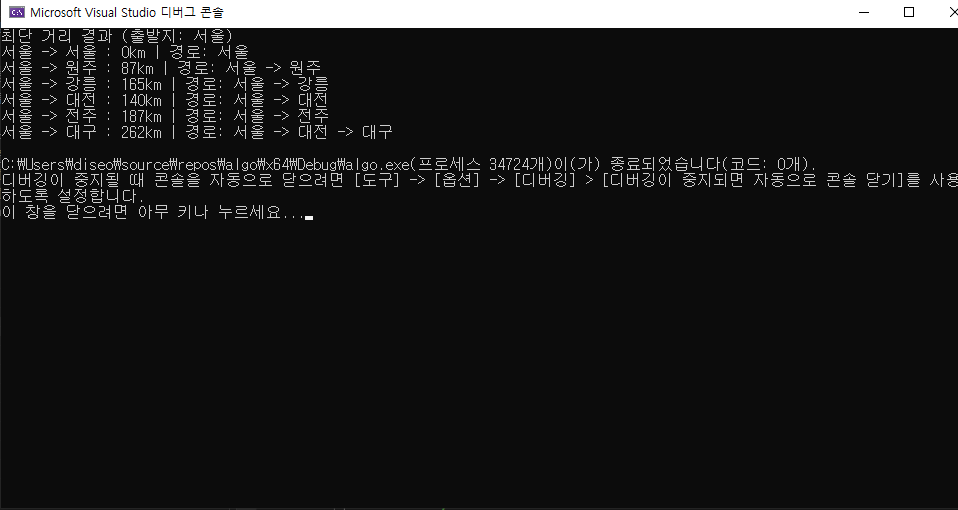
        cout << "최단 거리 결과 (출발지: " << vertices[here].name << ")" << endl;
        for (int i = 0; i < 6; ++i) {
            cout << vertices[here].name << " -> " << vertices[i].name << " : ";
            if (vertices[i].cost == INT32_MAX) {
                cout << "도달 불가" << endl;
                continue;
            }

            cout << vertices[i].cost << "km | 경로: ";

            stack<string> path;
            int current = i;
            while (current != here) {
                path.push(vertices[current].name);
                current = parent[current];
            }
            path.push(vertices[here].name);

            while (!path.empty()) {
                cout << path.top();
                path.pop();
                if (!path.empty()) cout << " -> ";
            }
            cout << endl;
        }
    }
};

출력 결과

int main() {
	DIJKSTRA D;
	D.CreateGraph();
	D.Dijkstra(0); // 서울에서 출발
	return 0;
}

✅ Prim 알고리즘이란?

모든 정점을 최소 비용으로 연결하는
**최소 신장 트리(MST, Minimum Spanning Tree)**를 만드는 알고리즘

✅ 핵심 개념

하나의 정점에서 시작해서
MST에 포함되지 않은 정점 중 가장 싼 간선을 반복적으로 선택
선택된 간선을 통해 트리를 확장
우선순위 큐(Min Heap)를 이용해 효율적으로 구현 가능

✅ 특징 요약

알고리즘 유형 : 탐욕 알고리즘 (Greedy)
그래프 조건 : 무방향 그래프, 연결 그래프
시간 복잡도 : O(E log V) (우선순위 큐 + 인접 리스트 사용 시)
자료구조 : 우선순위 큐, MST 포함 여부 배열, 비용 배열
적용 분야 : 네트워크 구축 비용 최소화, 전기 회로 설계, 도로 연결 최적화 등

✅ 장점

모든 정점을 사이클 없이 연결 가능
가중치가 양수인 무방향 그래프에서 항상 동작
시작점 하나만 정해주면 자동으로 전체 MST 구성

✅ 단점

간선 수가 적은 그래프에선 Kruskal 알고리즘이 더 효율적일 수 있음
가중치가 음수여도 가능하지만 MST 정의 상 무의미할 수도 있음
구현 시 MST 포함 여부나 간선 비용 갱신 처리가 조금 번거로울 수 있음

Prim

#pragma once
#include <iostream>
#include <vector>
#include <queue>
#include <string>

using namespace std;

class PRIM
{
public:
    struct Vertex {
        string name;
        bool inMST = false;
    };

    vector<Vertex> vertices;
    vector<vector<int>> adjacent;

    void CreateGraph() {
        vertices = {
            {"서울"}, {"원주"}, {"강릉"}, {"대전"}, {"전주"}, {"대구"}
        };

        adjacent = vector<vector<int>>(6, vector<int>(6, -1));

        adjacent[0][1] = 87;
        adjacent[0][2] = 165;
        adjacent[0][3] = 140;
        adjacent[0][4] = 187;

        adjacent[1][0] = 87;
        adjacent[1][2] = 95;
        adjacent[1][3] = 118;
        adjacent[1][5] = 178;

        adjacent[2][0] = 165;
        adjacent[2][1] = 95;
        adjacent[2][5] = 212;

        adjacent[3][0] = 140;
        adjacent[3][1] = 118;
        adjacent[3][4] = 56;
        adjacent[3][5] = 122;

        adjacent[4][0] = 187;
        adjacent[4][3] = 56;
        adjacent[4][5] = 130;

        adjacent[5][1] = 178;
        adjacent[5][2] = 212;
        adjacent[5][3] = 122;
        adjacent[5][4] = 130;
    }

    void Prim(int start) {
        int totalCost = 0;
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq; // (cost, to)

        pq.push({ 0, start });

        while (!pq.empty()) 
        {
            auto [cost, now] = pq.top(); 
            pq.pop();

            if (vertices[now].inMST) 
                continue;

            vertices[now].inMST = true;
            totalCost += cost;
            cout << "선택된 도시: " << vertices[now].name << " (비용: " << cost << ")" << endl;

            for (int there = 0; there < vertices.size(); ++there) {
                if (adjacent[now][there] == -1 || vertices[there].inMST) continue;
                pq.push({ adjacent[now][there], there });
            }
        }

        cout << "총 최소 비용: " << totalCost << endl;
    }

};

출력 결과

int main() {
	PRIM P;
	P.CreateGraph();
	P.Prim(0); // 서울에서 시작
	return 0;
}

✅ Ford-Fulkerson 알고리즘이란?

흐를 수 있는 경로(증가 경로)를 찾아 유량을 반복적으로 보내며,
최대 유량(Maximum Flow)을 계산하는 알고리즘

✅ 핵심 개념

유량이 흐를 수 있는 경로(잔여 용량 > 0)를 DFS 또는 BFS로 탐색
해당 경로에 가능한 만큼 유량을 보냄
이런 과정을 경로가 더 이상 없을 때까지 반복
역방향 유량도 고려 (되돌릴 수 있도록)

✅ 특징 요약

알고리즘 유형 : 그리디 + 네트워크 플로우
그래프 조건 : 방향 그래프 + 간선에 용량이 존재해야 함
시간 복잡도 : O(E × max_flow) (단순 DFS 사용 시)
자료구조 : 잔여 용량 배열, 유량 배열, 방문 배열
적용 분야 : 네트워크 최대 전송량, 작업 배정, 이분 매칭 등

✅ 장점

아이디어가 간단하고 직관적
최대 유량 보장 (정확한 답)
다양한 문제(이분 매칭 등)로 응용 가능성 매우 높음

✅ 단점

무한 루프 발생 가능성 있음 (소수점 유량일 때)
시간 복잡도가 높음 (max_flow에 비례)
안정적 성능을 원할 경우 BFS 기반 Edmonds-Karp 알고리즘 사용 권장

Ford Fulkerson

#include <iostream>
#include <vector>
#include <queue>
#include <climits>
using namespace std;

const int V = 6; // 정점 수 (0 ~ V-1)

class FORDFULKERSON
{
public:
    int capacity[V][V]; // 간선 용량
    int flow[V][V];     // 현재 유량
    bool visited[V];

    FORDFULKERSON() {
        for (int i = 0; i < V; ++i) {
            for (int j = 0; j < V; ++j) {
                capacity[i][j] = 0;
                flow[i][j] = 0;
            }
        }
    }

    // DFS로 증가 경로 찾기
    int dfs(int u, int t, int f) {
        if (u == t) return f;
        visited[u] = true;
        for (int v = 0; v < V; ++v) {
            int residual = capacity[u][v] - flow[u][v];
            if (!visited[v] && residual > 0) {
                int d = dfs(v, t, min(f, residual));
                if (d > 0) {
                    flow[u][v] += d;
                    flow[v][u] -= d; // 역방향 처리
                    return d;
                }
            }
        }
        return 0;
    }

    int fordFulkerson(int s, int t) {
        int maxFlow = 0;
        int f = 0;
        while (true) {
            memset(visited, false, sizeof(visited));
            f = dfs(s, t, INT_MAX);
            if (f == 0) break;
            maxFlow += f;
        }
        return maxFlow;
    }
};

출력 결과

int main() {
	FORDFULKERSON ff;

	// 예제 간선 설정
	ff.capacity[0][1] = 10;
	ff.capacity[0][2] = 10;
	ff.capacity[1][2] = 2;
	ff.capacity[1][3] = 4;
	ff.capacity[1][4] = 8;
	ff.capacity[2][4] = 9;
	ff.capacity[3][5] = 10;
	ff.capacity[4][3] = 6;
	ff.capacity[4][5] = 10;

	int source = 0, sink = 5;
	int result = ff.fordFulkerson(source, sink);
	cout << "최대 유량: " << result << endl;

	return 0;
}

인프런 워밍업 클럽 4기 CS 전공지식 3주차 발자국

컴퓨터 구조

✅ 프로그램 실행 구조

✅ 명령어 종류 요약

✅ 분기 명령어

✅ 제어 장치/출력 구성

✅ 기계어 vs 어셈블리어

자료구조와 알고리즘

✅ Trie란?

✅ 핵심 개념

✅ 특징 요약

✅ 장점

✅ 단점

✅ 그래프(Graph)란?

✅ DFS (깊이 우선 탐색)

✅ BFS (너비 우선 탐색)

✅ DFS vs BFS 요약 비교

✅ 다익스트라 알고리즘이란?

✅ 핵심 개념

✅ 특징 요약

✅ 장점

✅ 단점

✅ Prim 알고리즘이란?

✅ 핵심 개념

✅ 특징 요약

✅ 장점

✅ 단점

✅ Ford-Fulkerson 알고리즘이란?

✅ 핵심 개념

✅ 특징 요약

✅ 장점

✅ 단점