인프런 워밍업 클럽 4기 - CS 전공지식; 컴퓨터 구조 미션 1
9개월 전
미션 1 - 4입력 AND, OR, NAND, NOR, XOR 연산의 진리표를 작성해보세요.
답.
| A | B | C | D | AND | OR | NAND | NOR | XOR |
|:-:|:-:|:-:|:-:|:---:|:--:|:----:|:---:|:---:|
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
다음 불 방정식들을 여러 방법을 이용해 간략화 해보세요.
1. A( (BB)’+ 0A) + (CC)' = (AB’) +C 2. (B’B’) + (AD’ + (CA)’)D = B’ + (DC’) + (DA’) 3. (A’B) + B(B1 + BC) = B 4. B’(1C + BD) + DB = (B’C) + (DB)답.
1. A((BB)’ + 0A) + (CC)’ = AB’ + C’ ️(1) BB = B → (BB)’ = B’ (동일 법칙 + 여법칙) ️(2) 0A = 0 (항등법칙) ️(3) A(B’ + 0) = AB’ (항등원 + 분배법칙) ️(4) CC = C → (CC)’ = C’ (동일 법칙 + 여법칙) ️(5) AB’ + C’ 2. (B’B’) + (AD’ + (CA)’)D = B’ + DC’ + DA’ (1) B’·B’ = B’ (동일 법칙) ️(2) (CA)’ = C’ + A’ (드모르간 법칙) ️(3) AD’ + (C’ + A’) = AD’ + C’ + A’ → (AD’ + C’ + A’)D = AD’·D + C’·D + A’·D (분배법칙) ️(4) AD’·D = AD’, 나머지도 그대로 → AD’ + C’D + A’D (5) B’ + AD’ + C’D + A’D → 항 재정렬하면: B’ + C’D + A’D + AD’ = B’ + DC’ + DA’ 3. (A’B) + B(B1 + BC) = B ️(1) B·1 = B → B1 = B (항등법칙) ️(2) B + BC = B (흡수법칙) → B(B1 + BC) = B ️(3) (A’B) + B = B (흡수법칙 또는 결합) 4. B’(1C + BD) + DB = B’C + DB (1) 1C = C (항등법칙) → (1C + BD) = (C + BD) (2) B’(C + BD) = B’C + B’BD (분배법칙) (3) B’·B = 0 → B’BD = 0·D = 0 → B’C + 0 + DB = B’C + DB
3. 다음 2진수를 10진수로 변환해보세요.
1. 110111 =
2. 10000001 =
3. 11111100000 =
4. 101010 =답.
1. 110111 = 55
→ 2진수 110111은 (1×2⁵) + (1×2⁴) + (0×2³) + (1×2²) + (1×2¹) + (1×2⁰)
= 32 + 16 + 0 + 4 + 2 + 1 = 55
2. 10000001 = 129
→ 2진수 10000001은 (1×2⁷) + (0×2⁶) + ... + (0×2¹) + (1×2⁰)
= 128 + 0 + 0 + 0 + 0 + 0 + 0 + 1 = 129
3. 11111100000 = 2016
→ 2진수 11111100000은 (1×2¹⁰) + (1×2⁹) + (1×2⁸) + (1×2⁷) + (1×2⁶) + (1×2⁵)
나머지는 0이므로 계산 안 해도 됨
= 1024 + 512 + 256 + 128 + 64 + 32 = 2016
4. 101010 = 42
→ 2진수 101010은 (1×2⁵) + (0×2⁴) + (1×2³) + (0×2²) + (1×2¹) + (0×2⁰)
= 32 + 0 + 8 + 0 + 2 + 0 = 42
다음 10진수를 2진수로 변환해보세요.
1. 10 =
2. 27 =
3. 86 =
4. 516 =답.
1. 10 = 1010
→ 10 ÷ 2 = 5 ... 0
5 ÷ 2 = 2 ... 1
2 ÷ 2 = 1 ... 0
1 ÷ 2 = 0 ... 1
→ 역순으로 읽으면 1010(2)
2. 27 = 11011
→ 27 ÷ 2 = 13 ... 1
13 ÷ 2 = 6 ... 1
6 ÷ 2 = 3 ... 0
3 ÷ 2 = 1 ... 1
1 ÷ 2 = 0 ... 1
→ 역순으로 읽으면 11011(2)
3. 86 = 1010110
→ 86 ÷ 2 = 43 ... 0
43 ÷ 2 = 21 ... 1
21 ÷ 2 = 10 ... 1
10 ÷ 2 = 5 ... 0
5 ÷ 2 = 2 ... 1
2 ÷ 2 = 1 ... 0
1 ÷ 2 = 0 ... 1
→ 역순으로 읽으면 1010110(2)
4. 516 = 1000000100
→ 516 ÷ 2 = 258 ... 0
258 ÷ 2 = 129 ... 0
129 ÷ 2 = 64 ... 1
64 ÷ 2 = 32 ... 0
32 ÷ 2 = 16 ... 0
16 ÷ 2 = 8 ... 0
8 ÷ 2 = 4 ... 0
4 ÷ 2 = 2 ... 0
2 ÷ 2 = 1 ... 0
1 ÷ 2 = 0 ... 1
→ 역순으로 읽으면 1000000100(2)
다음 불 방정식을 logisim을 이용해 회로를 만들어보세요.(회로 이미지와 .circ파일 첨부)
다음 불 방정식을 logisim을 이용해 회로를 만들어보세요.(회로 이미지와 .circ파일 첨부),
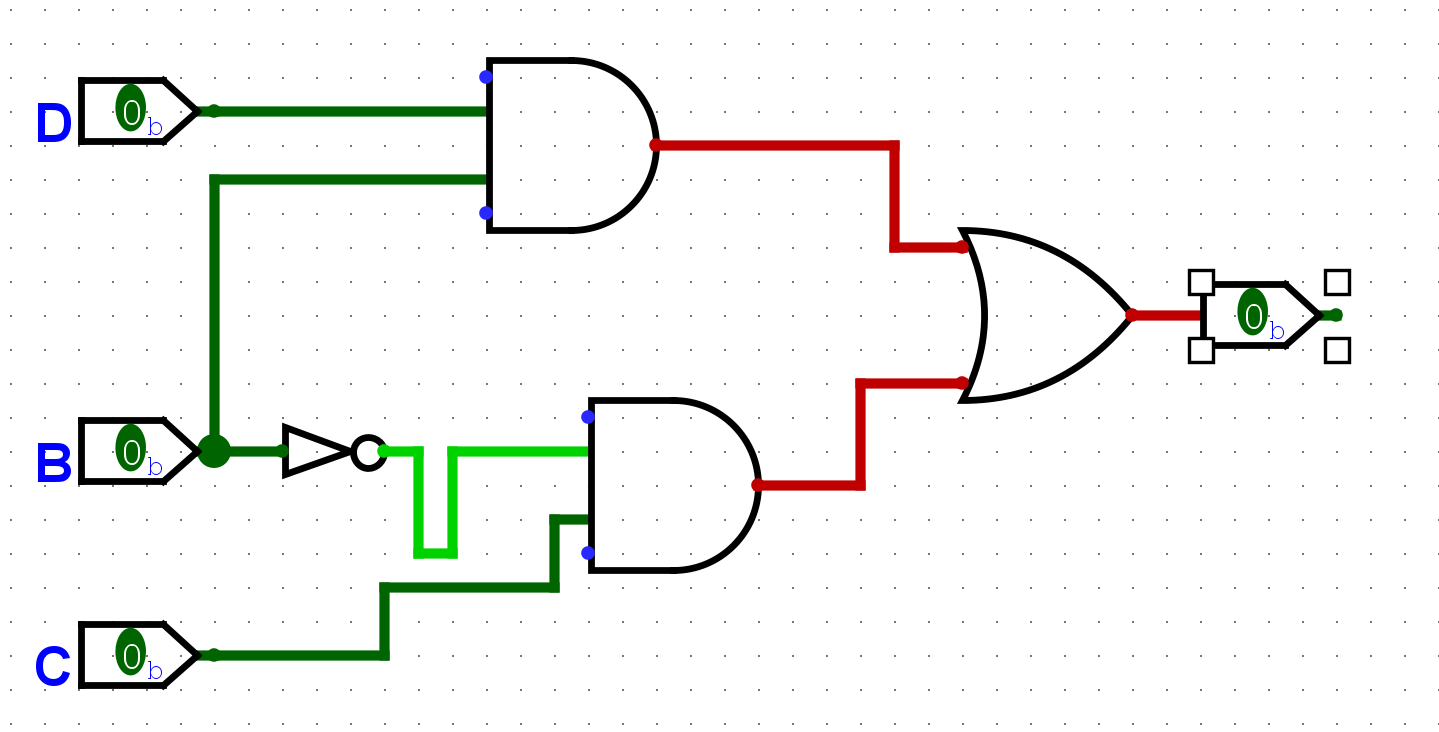
1. (B’C) + (DB)
2. (AB’) +C
3. B’ + (DC’) + (DA’)답.
댓글을 작성해보세요.
